

5.3.1 函数的单调性
新课程标准解读 | 核心素养 |
1.结合实例,借助几何直观了解函数的单调性与导数的关系 | 数学抽象、直观想象 |
2.能利用导数研究函数的单调性 | 逻辑推理、数学运算 |
3.对于多项式函数,能求不超过三次的多项式函数的单调区间 | 数学运算 |
第1课时导数与函数的单调性


研究股票时,我们最关心的是股票的发展趋势(走高或走低)以及股票价格的变化范围(封顶或保底).从股票走势曲线图来看,股票有升有降.在数学上,函数曲线也有升有降,就是我们常说的单调性.
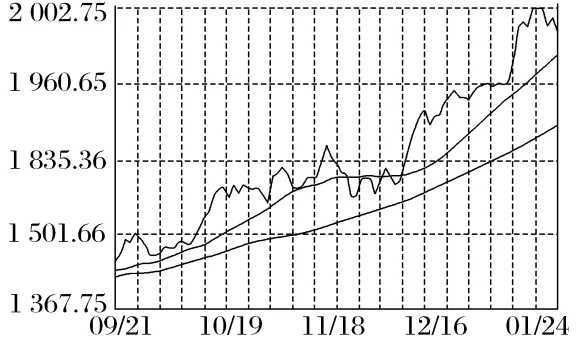
【问题】函数的单调性与导数有什么关系?

知识点一函数的单调性与导数的关系
定义在区间(a,b)内的函数y=f(x):
f'(x)的正负 | f(x)的单调性 |
f'(x)>0 | 单调递 增 |
f'(x)<0 | 单调递 减 |
提醒若在某区间内有有限个点使f'(x)=0,在其余的点恒有f'(x)>0(<0),则f(x)在该区间上单调递增(递减).
知识点二 函数值变化快慢与导数的关系
设函数y=f(x),在区间(a,b)上:
导数的绝对值 | 函数值变化 | 函数的图象 |
越大 | 快 | 比较“ 陡峭 ”(向上或向下) |
越小 | 慢 | 比较“ 平缓 ”(向上或向下) |

1.判断正误.(正确的画“√”,错误的画“×”)
(1)函数f(x)在定义域上都有f'(x)<0,则函数f(x)在定义域上是减函数.(×)
(2)函数f(x)在某区间内单调递增,则一定有f'(x)>0.(×)
(3)函数在某个区间上变化越快,函数在这个区间上的导数的绝对值越大.(√)
2.函数f(x)=ln x-x的单调递增区间是()
A.(0,1)B.(0,+∞)
C.(1,2)D.(2,+∞)
解析:A f'(x)=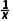 -1,令f'(x)>0,又x>0,∴0<x<1,则f(x)的单调递增区间是(0,1).
-1,令f'(x)>0,又x>0,∴0<x<1,则f(x)的单调递增区间是(0,1).
3.函数f(x)=cos x-x在(0,π)上的单调性是()
A.先增后减B.先减后增
C.单调递增D.单调递减
解析:D易知f'(x)=-sinx-1,x∈(0,π),∴f'(x)<0,则f(x)=cosx-x在(0,π)上单调递减.

【例1】(1)下列函数中,在(1,+∞)上单调递增的是()
A.y=x3-3xB.y=ln x-x
C.y=x+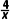 D.y=x2-3x+1
D.y=x2-3x+1
(2)(2024·枣庄月考)函数y=xln x在(0,5)上的单调性是()
A.单调递增
B.单调递减
C.在(0,)上单调递减,在(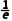 )上单调递增
)上单调递增
D.在(0,)上单调递增,在(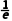 )上单调递减
)上单调递减
答案:(1)A(2)C
解析:(1)由y=x3-3x可得y'=3x2-3,当x∈(1,+∞)时,y'>0,y=x3-3x单调递增,故A满足题意;由y=lnx-x可得y'=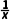 -1,当x∈(1,+∞)时,y'<0,y=lnx-x单调递减,故B不满足题意;易知y=x+
-1,当x∈(1,+∞)时,y'<0,y=lnx-x单调递减,故B不满足题意;易知y=x+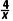 在(1,2)上单调递减,在(2,+∞)上单调递增,故C不满足题意;易知y=x2-3x+1在(1,)上单调递减,在(
在(1,2)上单调递减,在(2,+∞)上单调递增,故C不满足题意;易知y=x2-3x+1在(1,)上单调递减,在(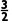 ,+∞)上单调递增,故D不满足题意,故选A.
,+∞)上单调递增,故D不满足题意,故选A.
(2)由已知得函数y=xlnx的定义域为(0,+∞).y'=lnx+1,令y'>0,得x>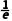 ;令y'<0,得0<x<
;令y'<0,得0<x<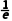 .∴函数y=xlnx在(0,)上单调递减,在(
.∴函数y=xlnx在(0,)上单调递减,在(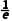 )上单调递增.
)上单调递增.
通性通法
利用导数判断函数的单调性的策略
利用导数证明或判断一个可导函数在给定区间内的单调性,实质上就是判断f'(x)的正负或证明不等式f'(x)≥0(或f'(x)≤0)在给定区间内恒成立.一般步骤为:①求导数f'(x);②判断f'(x)的符号;③得出结论.
【跟踪训练】
(多选)下列函数中,既是奇函数又在区间(0,1)上单调递增的是()
A.y=2x3+4xB.y=x+sin(-x)
C.y=log2|x|D.y=2x-2-x
解析:ABD由奇函数的定义可知,A、B、D均为奇函数,C为偶函数,所以排除C;对于选项A,y'=6x2+4>0,所以y=2x3+4x在(0,1)上单调递增;对于选项B,y'=1-cos(-x)≥0,且y'不恒为0,所以y=x+sin(-x)在(0,1)上单调递增;对于选项D,y'=2xln2+2-xln2>0,所以y=2x-2-x在(0,1)上单调递增.故选A、B、D.
【例2】求下列函数的单调区间:
(1)f(x)=x3-4x2+4x-1;
(2)f(x)=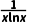 (x>0且x≠1).
(x>0且x≠1).
解:(1)函数f(x)的定义域为R,f'(x)=3x2-8x+4.
令3x2-8x+4=0,解得x=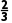 或x=2.
或x=2.
当x变化时,f'(x)与f(x)的变化情况如表所示:
x | (-∞,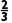 ) ) | 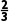
| (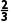 ) ) | 2 | (2,+∞) |
f'(x) | + | 0 | - | 0 | + |
f(x) | 单调递增 | f(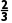 ) ) | 单调递减 | f(2) | 单调递增 |
所以函数f(x)的单调递增区间为(-∞,)和(2,+∞),单调递减区间为(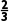 ).
).
(2)法一(列表法)函数的定义域为(0,1)∪(1,+∞),f'(x)=-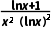
令f'(x)=0,得x=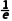 .
.
列表如下:
x | (0,) | 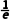
| (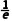 ) ) | (1,+∞) |
f'(x) | + | 0 | - | - |
f(x) | 单调递增 | f(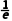 ) ) | 单调递减 | 单调递减 |
所以f(x)的单调递增区间是(0,),单调递减区间是(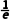 ),(1,+∞).
),(1,+∞).
法二(解不等式法)函数的定义域为(0,1)∪(1,+∞),f'(x)=-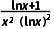
由f'(x)>0,得lnx+1<0,所以0<x<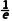 .
.
由f'(x)<0,得lnx+1>0,所以x>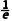 .
.
又因为x≠1,所以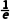 <x<1或x>1.
<x<1或x>1.
所以f(x)的单调递增区间是(0,),单调递减区间是(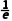 )和(1,+∞).
)和(1,+∞).
通性通法
利用导数求函数单调区间的方法
(1)列表法:①求定义域:确定函数f(x)的定义域;②求导:求f'(x);③确定零点:判断导函数f'(x)有无零点,若有零点,通过解方程f'(x)=0求出零点;④列表:用f'(x)的零点和函数的无定义点将f(x)的定义域划分为若干个区间,列表给出f'(x)在各区间上的正负;⑤得结论:由此得出函数f(x)在定义域内的单调性.
(2)解不等式法:①求定义域:确定函数f(x)的定义域;②求导:求f'(x);③解不等式:在定义域内,令f'(x)>0,解得函数f(x)的单调递增区间;令f'(x)<0,解得函数f(x)的单调递减区间.
【跟踪训练】
求下列函数的单调区间:
(1)f(x)=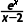 ;
;
(2)f(x)=2x2-ln x.
解:(1)函数f(x)的定义域为(-∞,2)∪(2,+∞).
f'(x)=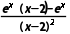 =
=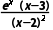 .因为x∈(-∞,2)∪(2,+∞),所以ex>0,(x-2)2>0.
.因为x∈(-∞,2)∪(2,+∞),所以ex>0,(x-2)2>0.
令f'(x)=0可得x=3,则f'(x)在各区间的正负,以及f(x)的单调性如表所示:
x | (-∞,2) | (2,3) | 3 | (3,+∞) |
f'(x) | - | - | 0 | + |
f(x) | 单调递减 | 单调递减 | f(3)=e3 | 单调递增 |
所以函数f(x)的单调递增区间为(3,+∞),单调递减区间为(-∞,2)和(2,3).
(2)函数f(x)=2x2-lnx的定义域为(0,+∞).
f'(x)=4x-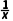 =
=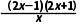 .
.
因为x>0,所以2x+1>0,由f'(x)>0,解得x>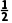 f(x)的单调递增区间为(
f(x)的单调递增区间为(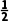 ,+∞);
,+∞);
由f'(x)<0,解得x<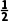 ,
,
又x∈(0,+∞),所以函数f(x)的单调递减区间为(0,).
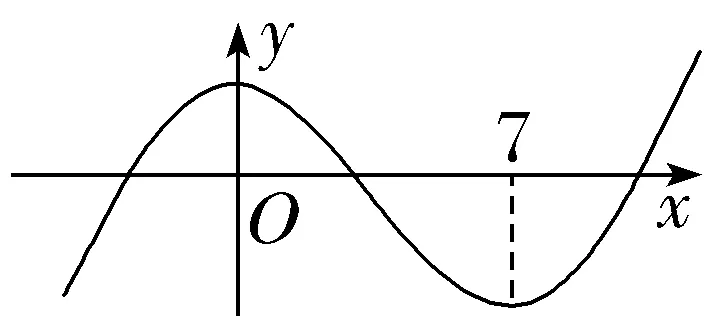
【例3】已知导函数f'(x)的下列信息:当x<0或x>7时,f'(x)>0;当0<x<7时,f'(x)<0;当x=0或x=7时,f'(x)=0,试画出函数f(x)的大致图象.
解:当x<0或x>7时,f'(x)>0,可知函数f(x)在区间(-∞,0)和(7,+∞)上都单调递增;当0<x<7时,f'(x)<0,可知函数f(x)在区间(0,7)上单调递减;当x=0或x=7时,f'(x)=0,这两个点比较特殊,我们称它们为“稳定点”.综上,函数f(x)的大致形状如图所示.
通性通法
研究函数图象与导函数图象之间关系的方法
导函数f'(x)图象在x轴上方时对应的自变量的取值区间为原函数f(x)图象上升部分对应的区间(单调递增区间),导函数f'(x)图象在x轴下方时对应的自变量的取值区间为原函数f(x)图象下降部分对应的区间(单调递减区间).
【跟踪训练】
1.(2024·宁德月考)函数y=f(x)的图象如图所示,则导函数y=f'(x)的图象可能是()
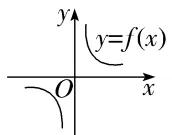
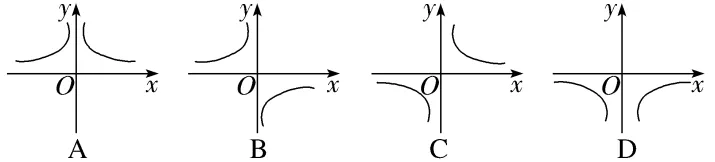
解析:D因为函数f(x)在(0,+∞),(-∞,0)上都单调递减,所以当x>0时f'(x)<0,当x<0时f'(x)<0.
2.已知f'(x)是f(x)的导函数,若f'(x)的图象如图所示,则f(x)的图象可能是()
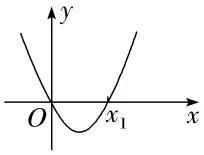
解析:C由导函数的图象可知,当x<0时,f'(x)>0,即函数f(x)单调递增;当0<x<x1时,f'(x)<0,即函数f(x)单调递减;当x>x1时,f'(x)>0,即函数f(x)单调递增.结合选项易知C正确.

1.函数f(x)=sin x-2x在(-∞,+∞)上()
A.是增函数B.是减函数
C.先增后减D.先减后增
解析:B∵f'(x)=cosx-2<0,∴f(x)在(-∞,+∞)上是减函数.
2.(2024·惠州月考)已知函数f(x)的导函数f'(x)的图象如图所示,则y=f(x)的图象可能为()
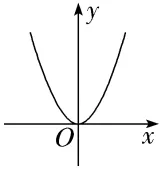
解析:D由导函数不是常数函数,排除A;由导函数f'(x)的图象可知,f'(x)≥0,当且仅当x=0时,f'(x)=0,所以函数f(x)是增函数,故排除C;又f'(0)=0,故排除B;满足条件的只有D.故选D.
3.函数f(x)=x3-3x的单调递减区间为(-1,1).
解析:对f(x)求导得f'(x)=3x2-3=3(x+1)(x-1),令f'(x)<0,解得-1<x<1.故f(x)的单调递减区间为(-1,1).
4.证明:函数f(x)=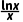 在区间(0,2)上单调递增.
在区间(0,2)上单调递增.
证明:由题意,得f'(x)=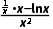 =
=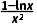 .
.
∵0<x<2,∴lnx<ln2<1,∴1-lnx>0,
∴f'(x)=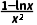 >0.
>0.
根据导数与函数单调性的关系,可知函数f(x)=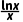 在区间(0,2)上单调递增.
在区间(0,2)上单调递增.


1.对于函数y=f(x),x∈(a,b),“f'(x)>0”是“函数y=f(x)为增函数”的()
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析:A由f'(x)>0⇒函数f(x)为增函数,但函数f(x)为增函数⇒/f'(x)>0,知“f'(x)>0”是“函数y=f(x)为增函数”的充分不必要条件.
2.已知函数f(x)=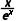 f(x)()
f(x)()
A.在(0,1)上单调递增
B.在(1,2)上单调递增
C.在(-∞,1)上单调递减
D.在(0,+∞)上单调递减
解析:A f'(x)=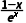 f'(x)>0得x<1,所以f(x)在(-∞,1)上单调递增,令f'(x)<0得x>1,所以f(x)在(1,+∞)上单调递减,故选A.
f'(x)>0得x<1,所以f(x)在(-∞,1)上单调递增,令f'(x)<0得x>1,所以f(x)在(1,+∞)上单调递减,故选A.
3.已知f(x)在R上是可导函数,f(x)的图象如图所示,则不等式f'(x)>0的解集为()
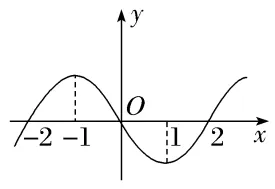
A.(-2,0)∪(2,+∞)B.(-∞,-2)∪(2,+∞)
C.(-∞,-1)∪(1,+∞)D.(-2,-1)∪(1,2)
解析:C因为f(x)在(-∞,-1),(1,+∞)上单调递增,所以f'(x)>0的解集为(-∞,-1)∪(1,+∞).
4.(2024·威海月考)函数f(x)=x-2sin x+1在(0,π)上的单调递增区间是()
A.(0,)B.(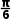 )
)
C.(0,)D.(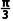 )
)
解析:D f(x)=x-2sinx+1,令f'(x)=1-2cosx>0,即cosx<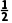 x∈(0,π),所以
x∈(0,π),所以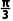 <x<π,故f(x)在(0,π)上的单调递增区间为(
<x<π,故f(x)在(0,π)上的单调递增区间为(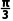 ).
).
5.(多选)下列函数在(-∞,+∞)上是单调函数的是()
A.y=x3+x-1B.y=sin x-x
C.y=xex+1D.y=ex-x
解析:AB由y=x3+x-1,得y'=3x2+1≥1,所以函数是增函数,A满足题意;由y=sinx-x,得y'=cosx-1≤0,所以函数是减函数,B满足题意;由y=xex+1,得y'=ex(x+1),当x≥-1时,y'=ex(x+1)≥0,函数单调递增,当x<-1时,y'=ex(x+1)<0,函数单调递减,故函数在(-∞,+∞)上不是单调函数,C不满足题意;由y=ex-x,得y'=ex-1,当x≥0时,y'=ex-1≥0,函数单调递增,当x<0时,y'=ex-1<0,函数单调递减,故函数在(-∞,+∞)上不是单调函数,D不满足题意.
6.(多选)设f'(x)是函数f(x)的导函数,将y=f(x)和y=f'(x)的图象画在同一个直角坐标系中,可能正确的是()
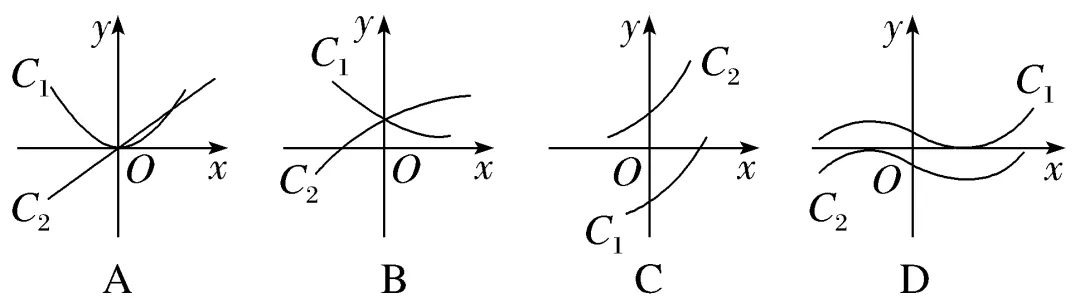
解析:ABCA、B、C均有可能;对于D,若C1为导函数,则y=f(x)应为增函数,不符合;若C2为导函数,则y=f(x)应为减函数,也不符合.
7.已知函数f(x)的导函数y=f'(x)的图象如图所示,则函数f(x)的单调递增区间是(-1,2),(4,+∞).
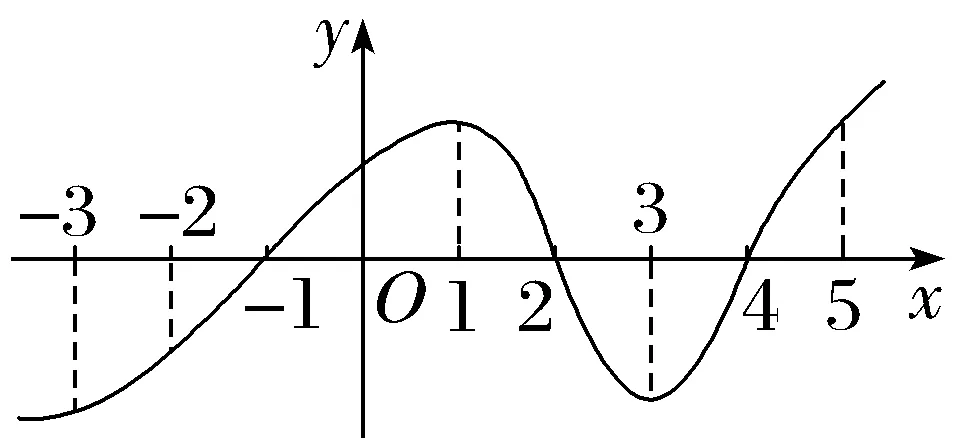
解析:由题图可知,在区间(-1,2),(4,+∞)上f'(x)>0;在区间(-∞,-1),(2,4)上f'(x)<0.由导函数的正负与函数单调性的关系可得,函数f(x)的单调递增区间是(-1,2),(4,+∞).
8.若函数f(x)的导函数为f'(x)=x2-4x+3,则函数f(1+x)的单调递减区间是(0,2).
解析:令f'(x)=x2-4x+3<0,得1<x<3,由1<1+x<3,解得0<x<2,故函数f(1+x)的单调递减区间为(0,2).
9.(2024·开封月考)函数f(x)=x2-5x+2ln(2x)的单调递增区间是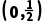 ,(2,+∞).
,(2,+∞).
解析:f(x)的定义域是(0,+∞),f'(x)=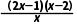 f'(x)>0得x>2或0<x<
f'(x)>0得x>2或0<x<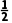 f(x)的单调递增区间是
f(x)的单调递增区间是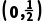 ,(2,+∞).
,(2,+∞).
10.判断函数f(x)=2x(ex-1)-x2的单调性.
解:函数f(x)的定义域为R,f'(x)=2(ex-1+xex-x)=2(ex-1)(x+1).
当x∈(-∞,-1)时,f'(x)>0;
当x∈(-1,0)时,f'(x)<0;
当x∈(0,+∞)时,f'(x)>0.
故f(x)在(-∞,-1)和(0,+∞)上单调递增,在(-1,0)上单调递减.

11.函数f(x)=xcos x的导函数f'(x)在区间[-π,π]上的图象大致是()
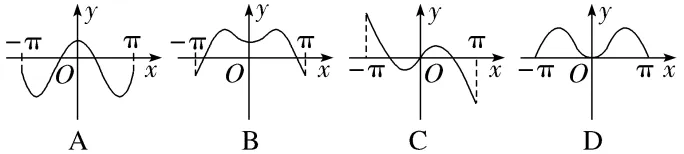
解析:A因为f(x)=xcosx,所以f'(x)=cosx-xsinx.因为f'(-x)=f'(x),所以f'(x)为偶函数,所以函数图象关于y轴对称.由f'(0)=1可排除C、D.而f'(1)=cos1-sin1<0,排除B.
12.定义在R上的可导函数f(x),已知y=ef'(x)的图象如图所示,则y=f(x)的单调递增区间是()
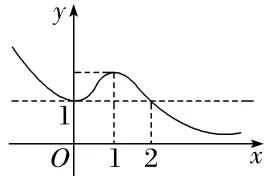
A.(-∞,1)B.(-∞,2)
C.(0,1)D.(1,2)
解析:B由题图知f'(x)≥0的区间是(-∞,2),故函数y=f(x)的单调递增区间为(-∞,2),故选B.
13.(2024·泉州月考)设函数f(x)=4ln x-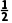 x2+3x在区间[a,a+1]上单调递增,则实数a的取值范围是()
x2+3x在区间[a,a+1]上单调递增,则实数a的取值范围是()
A.(0,3]B.(0,2]
C.[3,+∞)D.[2,+∞)
解析:A由函数f(x)=4lnx-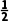 x2+3x,可得f'(x)=
x2+3x,可得f'(x)=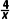 -x+3=
-x+3=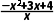 >0,令f'(x)≥0,即
>0,令f'(x)≥0,即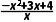 ≥0,即-x2+3x+4≥0,解得0<x≤4,所以函数f(x)在(0,4]上单调递增,又由函数f(x)在[a,a+1]上单调递增,所以
≥0,即-x2+3x+4≥0,解得0<x≤4,所以函数f(x)在(0,4]上单调递增,又由函数f(x)在[a,a+1]上单调递增,所以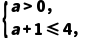 解得0<a≤3,故选A.
解得0<a≤3,故选A.
14.已知函数f(x)=ln x-x+1,x∈(0,+∞).
(1)讨论f(x)的单调性;
(2)利用(1)的结论证明当x∈(1,+∞)时ln x<x-1.
解:(1)∵f'(x)=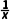 -1=
-1=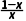
∴当x>1时,f'(x)<0;当0<x<1时,f'(x)>0.
∴f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞).
(2)证明:由(1)知f(x)=lnx-x+1在(1,+∞)上单调递减,
∴f(x)<f(1)=0,即lnx<x-1.

15.(多选)若函数f(x)在定义域D内的某个区间I上单调递增,且F(x)=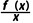 在区间I上也单调递增,则称y=f(x)是I上的“一致递增函数”.已知f(x)=x+
在区间I上也单调递增,则称y=f(x)是I上的“一致递增函数”.已知f(x)=x+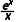 f(x)是区间I上的“一致递增函数”,则区间I可能是()
f(x)是区间I上的“一致递增函数”,则区间I可能是()
A.(-∞,-2)B.(-∞,0)
C.(0,+∞)D.(2,+∞)
解析:AD f(x)=x+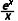 f'(x)=
f'(x)=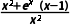 ;F(x)=
;F(x)=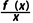 =1+
=1+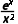 F'(x)=
F'(x)=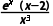 x∈(-∞,-2)时,f'(x)=
x∈(-∞,-2)时,f'(x)=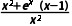 >
>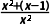 >0,函数单调递增,F'(x)=
>0,函数单调递增,F'(x)=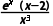 >0,函数单调递增,A满足;f'(-
>0,函数单调递增,A满足;f'(-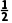 )=
)=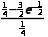 <0,故B不满足;F'(1)=-e<0,故C不满足;当x∈(2,+∞)时,f'(x)=
<0,故B不满足;F'(1)=-e<0,故C不满足;当x∈(2,+∞)时,f'(x)=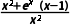 >0,函数单调递增,F'(x)=
>0,函数单调递增,F'(x)=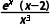 >0,函数单调递增,故D满足.
>0,函数单调递增,故D满足.
16.(2024·临沂质检)已知函数f(x)=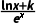 (k为常数,e为自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
(k为常数,e为自然对数的底数),曲线y=f(x)在点(1,f(1))处的切线与x轴平行.
(1)求实数k的值;
(2)求函数f(x)的单调区间.
解:(1)由f(x)=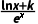 f'(x)=
f'(x)=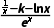 .
.
∵曲线y=f(x)在点(1,f(1))处的切线与x轴平行,
∴f'(1)=0,即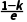 =0,解得k=1.
=0,解得k=1.
(2)由(1)知,f'(x)=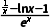 (x>0),
(x>0),
设h(x)=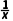 -lnx-1(x>0),则h'(x)=-
-lnx-1(x>0),则h'(x)=-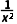 -
-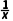 <0.
<0.
可知h(x)在(0,+∞)上是减函数,由h(1)=0知,
当0<x<1时,h(x)>h(1)=0,故f'(x)>0;
当x>1时,h(x)<h(1)=0,故f'(x)<0.
综上,f(x)的单调递增区间是(0,1),单调递减区间是(1,+∞).

通过网盘分享的文件:25-26学年同步培优讲义
链接: https://pan.baidu.com/s/1y0bSGZE1YoJg8gMTXiqQoA?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享