

培优课数列的函数特征

【例1】数列{an}满足an+1=1-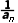 a1=2,则a20=()
a1=2,则a20=()
A.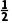 B.-1
B.-1
C.2D.1
解析:A由an+1=1-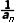 及a1=2,得a2=
及a1=2,得a2=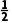 3=-1,a4=2,至此可发现数列{an}是周期为3的周期数列:2,,-1,2,,-1,….而20=6×3+2,故a20=a2=
3=-1,a4=2,至此可发现数列{an}是周期为3的周期数列:2,,-1,2,,-1,….而20=6×3+2,故a20=a2=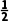 .
.
通性通法
利用数列的周期性求数列中某一项的步骤
(1)根据已知的数列的递推公式,写出数列的前几项,观察项与项之间的关系直至出现重复的项;
(2)确定该数列的周期;
(3)利用周期性求出要求的项.
【跟踪训练】
(2024·临沂质检)数列{an}满足a1=3,a2=6,an+2=an+1-an,则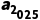 =3.
=3.
解析:由a1=3,a2=6,an+2=an+1-an,得a3=a2-a1=3,a4=a3-a2=-3,a5=a4-a3=-6,a6=a5-a4=-3,a7=a6-a5=3,a8=a7-a6=6,…,所以数列{an}是以6为周期的周期数列,所以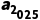 =a6×337+3=a3=3.
=a6×337+3=a3=3.
角度1数列单调性的判断
【例2】已知数列{an}的通项公式为an=3n2-n(n∈N*),判断该数列的单调性.
解:法一 an=3n2-n,an+1=3(n+1)2-(n+1),
则an+1-an=3(n+1)2-(n+1)-(3n2-n)=6n+2>0,
即an+1>an,故数列{an}是递增数列.
法二 an=3n2-n,an+1=3(n+1)2-(n+1),
则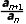 =
=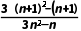 =
=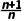 ·
·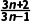 >1.
>1.
又易知an>0,故an+1>an,即数列{an}是递增数列.
通性通法
解决数列的单调性问题的两种方法
(1)作差比较法:根据an+1-an的符号判断数列{an}是递增数列、递减数列或是常数列;
(2)作商比较法:根据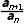 (an>0或an<0)与1的大小关系进行判断.
(an>0或an<0)与1的大小关系进行判断.
角度2数列单调性的应用
【例3】(2024·福州质检)已知数列{an}的通项公式为an=(n+1)·(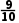 )n(n∈N*),试问该数列有没有最大项?若有,求出最大项和最大项的项数;若没有,说明理由.
)n(n∈N*),试问该数列有没有最大项?若有,求出最大项和最大项的项数;若没有,说明理由.
解:法一∵an+1-an=(n+2)(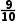 )n+1-(n+1)·(
)n+1-(n+1)·(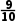 )n=(
)n=(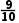 )n·
)n·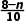 .
.
∴当n<8时,an+1-an>0,即an+1>an;
当n=8时,a9-a8=0,即a9=a8;
当n>8时,an+1-an<0,即an+1<an;
故a1<a2<…<a8=a9>a10>a11>…,
∴数列{an}中最大项为a8或a9,
其值为9·(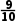 )8,其项数为8或9.
)8,其项数为8或9.
法二根据题意,令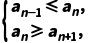
即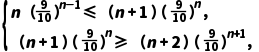
解得8≤n≤9.
又n∈N*,则n=8或n=9.
故数列{an}有最大项,为第8项和第9项,
且a8=a9=9·(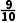 )8.
)8.
通性通法
求数列最大项与最小项的常用方法
(1)函数法:利用相关的函数求最值.若能借助表达式观察出单调性,直接确定最大(小)项,否则,利用作差法;
(2)利用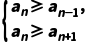 (n≥2)确定最大项,利用
(n≥2)确定最大项,利用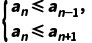 (n≥2)确定最小项.
(n≥2)确定最小项.
【跟踪训练】
1.若数列{an}的通项公式为an=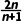 ()
()
A.递增数列B.递减数列
C.常数列D.以上都不是
解析:A因为an=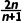 =2-
=2-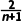 n≥2时,an-an-1=(2-
n≥2时,an-an-1=(2-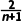 )-(2-
)-(2-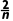 )=
)=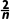 -
-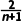 =
=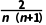 >0,所以数列{an}是递增数列.
>0,所以数列{an}是递增数列.
2.已知数列{an}的通项公式为an=n-7,则数列{nan}的最小项为第3或4项.
解析:nan=n(n-7)=n2-7n=(n-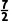 )2-
)2-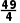 .因为n∈N*,所以当n=3或n=4时,数列{nan}的项最小.
.因为n∈N*,所以当n=3或n=4时,数列{nan}的项最小.

1.已知数列{an}满足an>0,且an+1=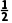 an,则数列{an}是()
an,则数列{an}是()
A.递增数列B.递减数列
C.常数列D.以上都不是
解析:B因为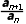 =
=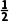 <1,an>0,所以an+1<an,故数列{an}为递减数列.
<1,an>0,所以an+1<an,故数列{an}为递减数列.
2.已知数列{an}满足an+1=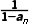 a1=
a1=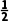 a2 025=()
a2 025=()
A.-1B.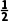
C.1D.2
解析:A由a1=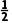 n+1=
n+1=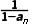 得a2=2,a3=-1,a4=
得a2=2,a3=-1,a4=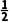 5=2,…,可知数列{an}是以3为周期的周期数列,因此a2025=a3×675=a3=-1.
5=2,…,可知数列{an}是以3为周期的周期数列,因此a2025=a3×675=a3=-1.
3.数列{-2n2+29n+3}中最大的项是()
A.107B.108
C.108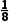 D.109
D.109
解析:B因为-2n2+29n+3=-2(n2-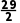 n)+3=-2(n-
n)+3=-2(n-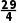 )2+
)2+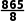 n=7时,-2n2+29n+3取得最大值108,故选B.
n=7时,-2n2+29n+3取得最大值108,故选B.
4.(2024·新乡质检)已知数列{an}中, an=k·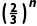 {an}是递增数列,试求实数k的取值范围.
{an}是递增数列,试求实数k的取值范围.
解:因为an=k·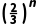 {an}是递增数列,所以an+1-an=k·
{an}是递增数列,所以an+1-an=k·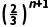 -k·
-k·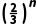 =
=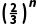 ·
·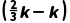 =-
=-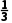 k·
k·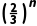 >0对任意的n∈N*恒成立,所以-
>0对任意的n∈N*恒成立,所以-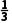 k>0,解得k<0,
k>0,解得k<0,
所以实数k的取值范围是 .
.

1.已知数列{an}的通项公式为an=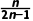 ()
()
A.递增数列B.递减数列
C.摆动数列D.常数列
解析:B因为an=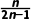 =
=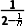 n的增大,2-
n的增大,2-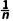 是递增的,故an是递减的,则数列{an}是递减数列,故选B.
是递增的,故an是递减的,则数列{an}是递减数列,故选B.
2.已知数列{an}中,a1=b(b为任意常数),an+1=-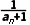 (n=1,2,3,…),则能使an=b的n的值是()
(n=1,2,3,…),则能使an=b的n的值是()
A.14B.15
C.16D.17
解析:C a2=-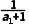 =-
=-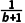 3=-
3=-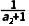 =-
=-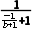 =-1-
=-1-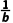 4=-
4=-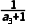 =-
=-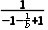 =b.可见{an}是以前三项为一个周期的周期数列,所以a1=a4=a7=a10=a13=a16=…=b.
=b.可见{an}是以前三项为一个周期的周期数列,所以a1=a4=a7=a10=a13=a16=…=b.
3.(2024·湖州月考)对任意的a1∈(0,1),由关系式an+1=f(an)得到的数列{an}满足an+1>an(n∈N*),则函数y=f(x)的图象可能是()
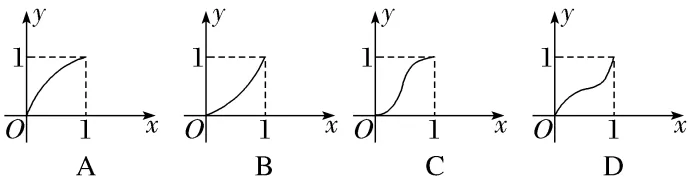
解析:A根据题意,由关系式an+1=f(an)得到的数列{an}满足an+1>an,即函数y=f(x)的图象上任一点(x,y)都满足y>x.结合图象,可知只有A满足,故选A.
4.已知数列{an}的通项公式为an=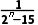 ()
()
A.1,-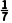 B.0,-
B.0,-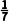
C.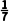 ,-
,-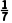 D.1,-
D.1,-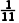
解析:A因为n∈N*,所以当1≤n≤3时,an=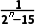 <0,且单调递减;当n≥4时,an=
<0,且单调递减;当n≥4时,an=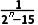 >0,且单调递减,所以最小项为a3=
>0,且单调递减,所以最小项为a3=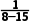 =-
=-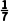 a4=
a4=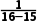 =1.故选A.
=1.故选A.
5.设数列{an}的通项公式为an=n2+bn,若数列{an}是递增数列,则实数b的取值范围为()
A.[1,+∞)B.[-2,+∞)
C.(-3,+∞)D.(-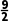 ,+∞)
,+∞)
解析:C因为函数f(n)=n2+bn图象的对称轴方程为n=-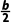 -
-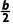 <
<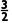 b>-3时,单调递增.
b>-3时,单调递增.
6.(多选)若数列{an}满足a1=1,a2=2,anan-2=an-1(n≥3),记数列{an}的前n项积为Tn,则下列说法正确的是()
A.Tn无最大值 B.an有最大值
C.T2 024=1D.a2 024=2
解析:BD∵a1=1,a2=2,anan-2=an-1(n≥3),∴a3=2,a4=1,a5=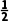 6=
6=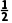 7=1,a8=2,…,因此数列{an}是周期为6的周期数列,an+6=an,∴an有最大值2,a2024=a2=2,又∵T1=1,T2=2,T3=4,T4=4,T5=2,T6=1,T7=1,T8=2,…,∴{Tn}是周期为6的周期数列,Tn+6=Tn,∴Tn有最大值4,T2024=T2=2.故选B、D.
7=1,a8=2,…,因此数列{an}是周期为6的周期数列,an+6=an,∴an有最大值2,a2024=a2=2,又∵T1=1,T2=2,T3=4,T4=4,T5=2,T6=1,T7=1,T8=2,…,∴{Tn}是周期为6的周期数列,Tn+6=Tn,∴Tn有最大值4,T2024=T2=2.故选B、D.
7.数列{(n-a)2}是递增数列,则实数a的取值范围是(-∞,).
解析:因为{(n-a)2}是递增数列,记an=(n-a)2,则an+1-an=(n+1-a)2-(n-a)2=2n+1-2a>0,所以a<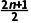 对任意的n∈N*恒成立,所以a<
对任意的n∈N*恒成立,所以a<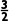 .
.
8.(2024·泉州月考)请写出一个符合下列要求的数列{an}的通项公式:①{an}为无穷数列;②{an}为单调递增数列;③0<an<2.这个数列的通项公式可以是an=2-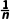 (答案不唯一).
(答案不唯一).
解析:因为函数an=2-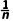 的定义域为N*,且an=2-
的定义域为N*,且an=2-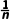 在N*上单调递增,0<2-
在N*上单调递增,0<2-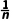 <2,所以满足3个条件的数列的通项公式可以是an=2-
<2,所以满足3个条件的数列的通项公式可以是an=2-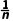 .
.
9.已知数列{an}的通项公式为an=|n-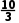 |,则an的最小项为
|,则an的最小项为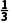 ,此时n的值为3.
,此时n的值为3.
解析:因为an=|n-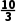 |,所以当n=1,2,3时,an=
|,所以当n=1,2,3时,an=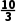 -n,此时an的最小项为
-n,此时an的最小项为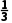 n=3;当n>3,n∈N*时,an=n-
n=3;当n>3,n∈N*时,an=n-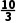 an的最小项为
an的最小项为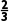 n=4.综上所述,an的最小项为
n=4.综上所述,an的最小项为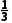 n=3.
n=3.
10.在数列{an}中,已知an=-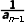 (n≥2,n∈N*).
(n≥2,n∈N*).
(1)求证an+2=an;
(2)若a4=4,求a20的值;
(3)若a1=1,求a1+a2+a3+a4+a5+a6+a7的值.
解:(1)证明:当n≥1时,因为an+2=an+1+1=-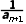 =-
=-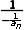 =an,所以an+2=an成立.
=an,所以an+2=an成立.
(2)由(1)知数列{an}是以2为周期的周期数列,所以a20=a4=4.
(3)因为a1=1,所以a2=-1,因为数列的周期为2,所以(a1+a2)+(a3+a4)+(a5+a6)+a7=a1=1.
11.已知函数f(x)=2x-2-x,数列{an}满足f(log2an)=-2n.
(1)求数列{an}的通项公式;
(2)讨论数列{an}的单调性,并证明你的结论.
解:(1)∵f(x)=2x-2-x,f(log2an)=-2n(an>0),∴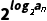 -
-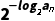 =-2n,∴an-
=-2n,∴an-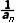 =-2n.∴
=-2n.∴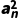 +2nan-1=0,解得an=-n±
+2nan-1=0,解得an=-n±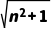 .∵an>0,∴an=
.∵an>0,∴an=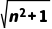 -n.
-n.
(2)∵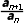 =
=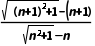 =
=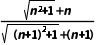 <1,an>0,∴an+1<an,∴数列{an}是递减数列.
<1,an>0,∴an+1<an,∴数列{an}是递减数列.
12.已知数列{an}中,an=1+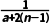 (n∈N*,a∈R且a≠0).
(n∈N*,a∈R且a≠0).
(1)若a=-7,求数列{an}中的最大项和最小项的值;
(2)若对任意的n∈N*,都有an≤a6成立,求a的取值范围.
解:(1)当a=-7时,an=1+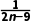 (n∈N*).
(n∈N*).
结合函数f(x)=1+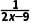 的单调性,
的单调性,
可知1>a1>a2>a3>a4,a5>a6>a7>…>an>1(n∈N*).
∴数列{an}中的最大项为a5=2,最小项为a4=0.
(2)an=1+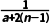 =1+
=1+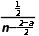
已知对任意的n∈N*,都有an≤a6成立,
结合函数f(x)=1+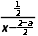 的单调性,
的单调性,
可知5<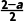 <6,即-10<a<-8,
<6,即-10<a<-8,
即a的取值范围是(-10,-8).