

第2课时直线与平面垂直的性质

1.已知平面α与两条直线l,m,l⊥α,则“m∥l”是“m⊥α”的()
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
2.已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()
A.α∥β,且l∥α
B.α⊥β,且l⊥β
C.α与β相交,且交线垂直于l
D.α与β相交,且交线平行于l
3.已知正方体ABCD-A1B1C1D1的棱长为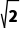 AB1D1到平面BC1D的距离为()
AB1D1到平面BC1D的距离为()
A.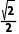 B.
B.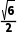 C.
C.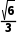 D.
D.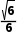
4.已知Rt△EFG的直角顶点E在平面α内,斜边FG∥α,且FG=6 cm,EF,EG与平面α分别成30°和45°角,则FG到平面α的距离是()
A.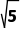 cm B.
cm B.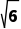 cm
cm
C.2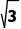 cmD.2
cmD.2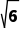 cm
cm
5.(多选)(2024·潮州月考)如图,PA⊥矩形ABCD所在的平面,则下列结论中正确的是()
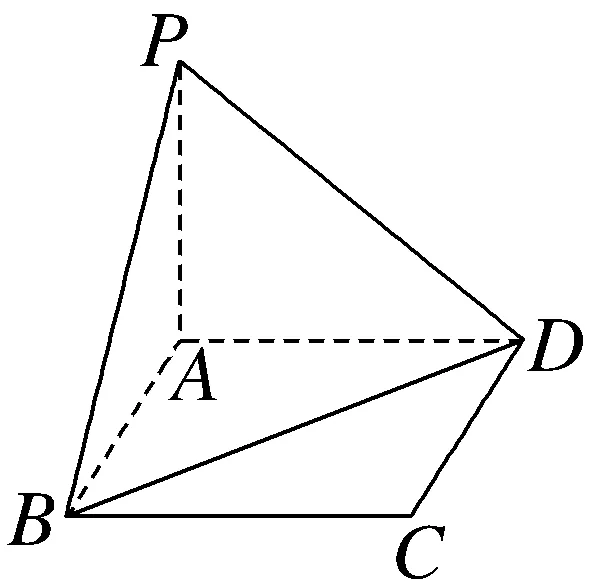
A.PB⊥BC
B.PD⊥CD
C.PD⊥BD
D.PA⊥BD
6.(多选)如图,ABCD是矩形,沿对角线BD将△ABD折起到△A'BD,且A'在平面BCD上的射影O恰好在CD上,则下列结论正确的是()
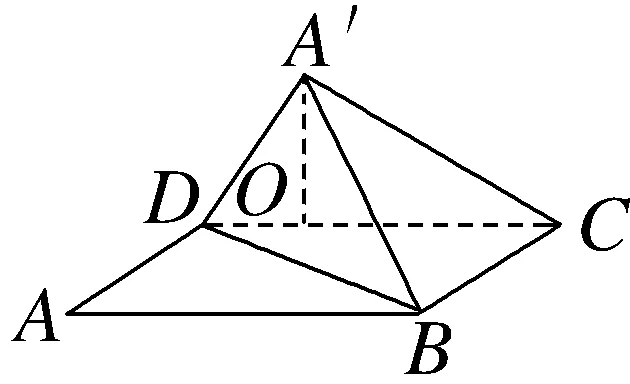
A.A'C⊥BDB.A'D⊥BC
C.A'C⊥BCD.A'D⊥A'B
7.在长方体ABCD-A1B1C1D1中,E∈BD,F∈B1D1,且EF⊥AB,则EF与AA1的位置关系是.
8.在长方体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=2.则直线AB到平面A1B1C1D1的距离为;平面ADD1A1与平面BCC1B1之间的距离为.
9.一条与平面α相交的线段,其长度为10 cm,两端点到平面α的距离分别是2 cm,3 cm,则这条线段与平面α所成角的大小是.
10.斜边为AB的Rt△ABC,PA⊥平面ABC.AE⊥PB,AF⊥PC,E,F分别为垂足,如图.
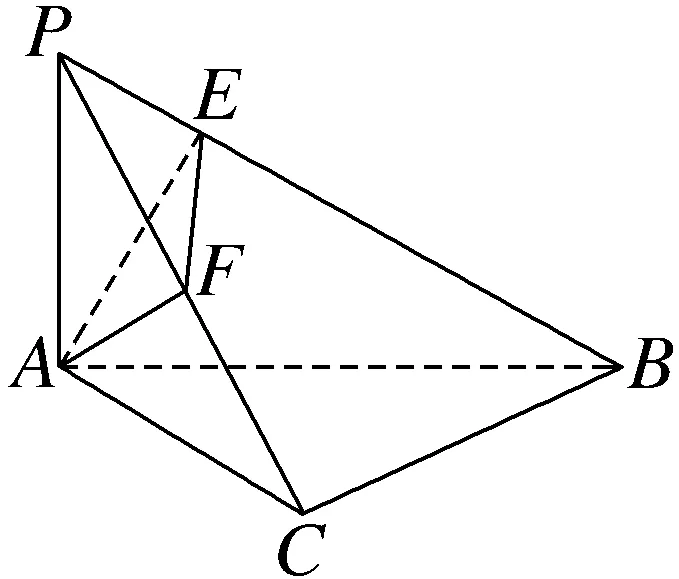
(1)求证:EF⊥PB;
(2)若直线l⊥平面AEF,求证:PB∥l.

11.如图,设平面α∩平面β=PQ,EG⊥平面α,FH⊥平面α,垂足分别为G,H.为使PQ⊥GH,则需增加的一个条件是()
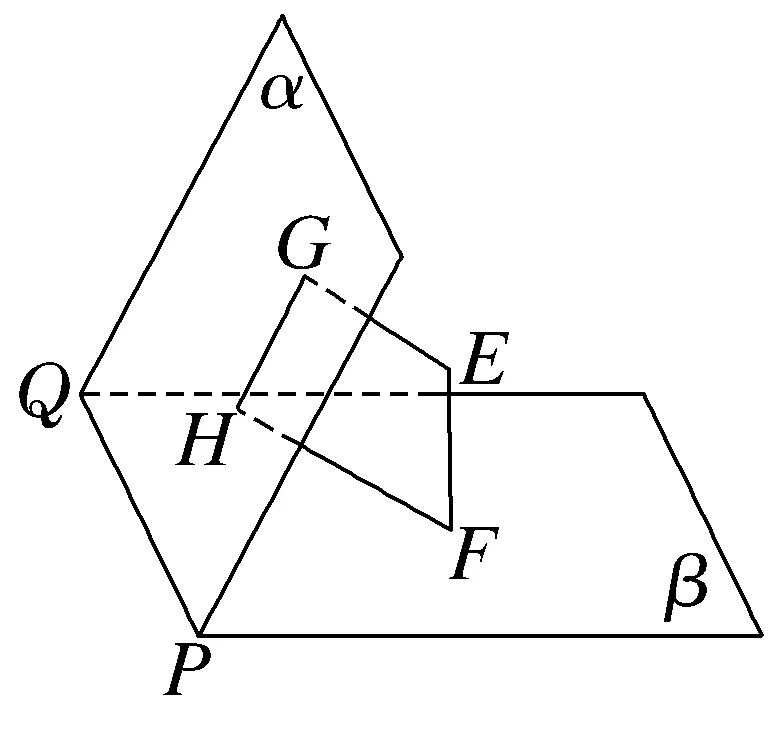
A.EF⊥平面α
B.EF⊥平面β
C.PQ⊥GE
D.PQ⊥FH
12.(多选)如图,等边三角形ABC的边长为1,BC边上的高为AD,沿AD把△ABC折起来,则()
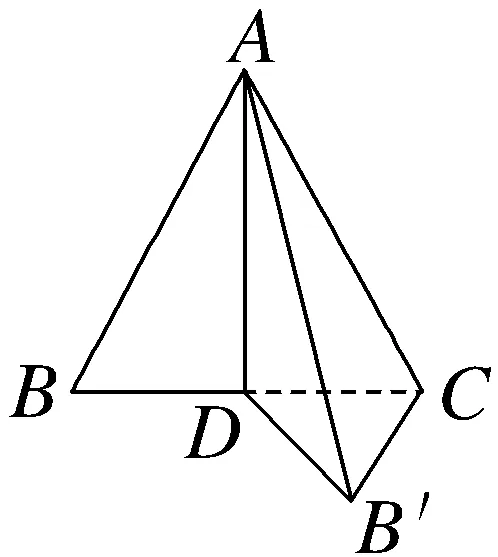
A.在折起的过程中始终有AD⊥平面DB'C
B.三棱锥A-DB'C的体积的最大值为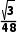
C.当∠B'DC=60°时,点A到B'C的距离为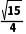
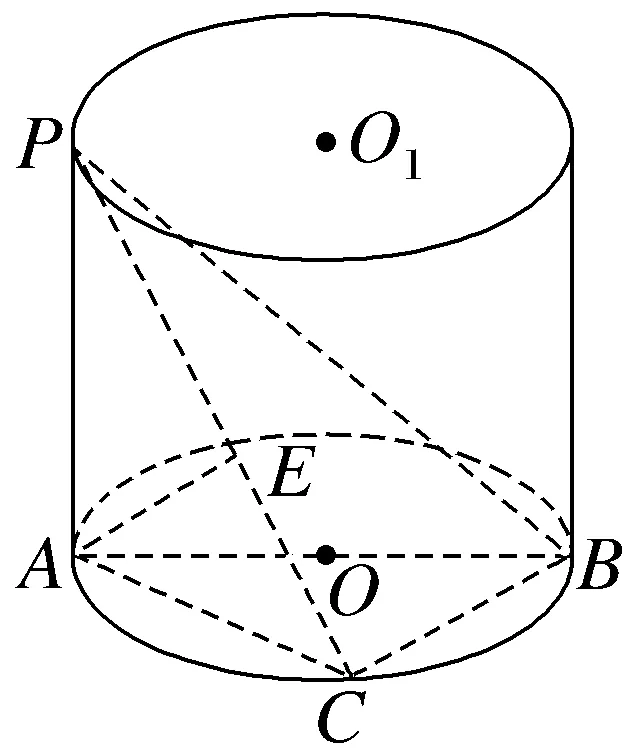
D.当∠B'DC=90°时,点C到平面ADB'的距离为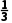
13.如图,在四棱锥P-ABCD中,已知底面ABCD是矩形,AB=2,AD=a,PD⊥平面ABCD,若边AB上存在点M,使得PM⊥CM,则实数a的取值范围是.
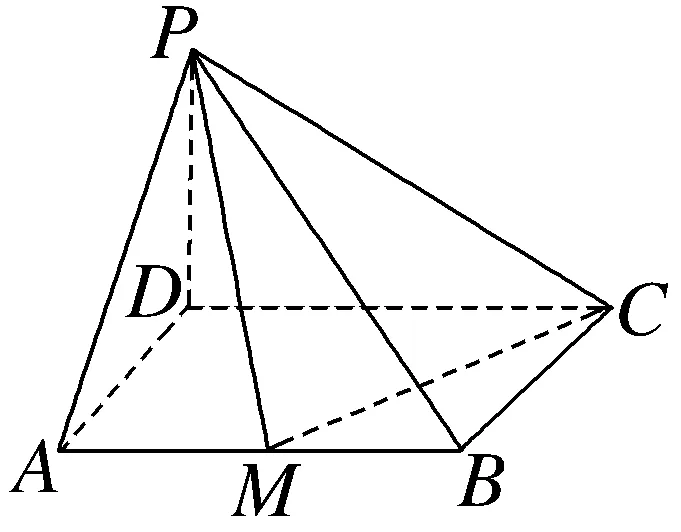
14.如图,已知AB为圆柱OO1底面圆O的直径,C为 的中点,点P为圆柱上底面圆O1上一点,PA⊥平面ABC,PA=AB,过点A作AE⊥PC,交PC于点E.
的中点,点P为圆柱上底面圆O1上一点,PA⊥平面ABC,PA=AB,过点A作AE⊥PC,交PC于点E.
(1)求证:AE⊥PB;
(2)若点C到平面PAB的距离为1,求圆柱OO1的表面积.

15.(2024·杭州月考)在△ABC中,∠ACB=90°,AB=8,∠BAC=60°,PC⊥平面ABC,PC=4,M是AB边上的一动点,则PM的最小值为()
A.2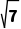 B.7
B.7
C.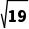 D.
D.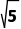
16.如图,在四面体P-ABC中,PA⊥平面ABC,PA=AB=1,BC=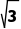 =2.
=2.
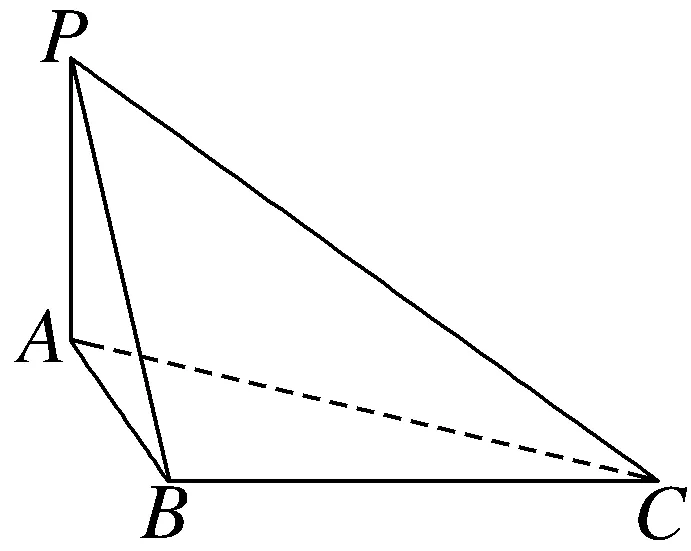
(1)证明:BC⊥平面PAB;
(2)在线段PC上是否存在点D,使得AC⊥BD?若存在,求出PD的值,若不存在,请说明理由.

通过网盘分享的文件:【免费下载】25-26学年同步培优讲义第2课时 直线与平面垂直的性质(学生版课时跟踪检测
链接: https://pan.baidu.com/s/1cTHdXyKyFz0oX0_OMWt9PA?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享