【免费下载】25-26学年同步培优讲义拓 视 野 欧拉公式及应用(学生版

欧拉公式及应用

欧拉公式e^ix＝cos x＋isin x（x∈R，i为虚数单位）是由瑞士著名数学家欧拉发明的，它将指数函数的定义域推广到复数，建立了三角函数与指数函数的关系，它在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”.

【例】（1）欧拉公式e^i θ＝cos θ＋isin θ把自然对数的底数e、虚数单位i、三角函数联系在一起，充分体现了数学的和谐美.若复数z满足（e^iπ＋i）·z＝i，则z的虚部为（）

A.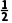B.－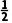

C.1D.－1

（2）（多选）欧拉公式e^xi＝cos x＋isin x（其中i为虚数单位，x∈R），依据欧拉公式，下列选项正确的是（）

A.复数e²ⁱ对应的点位于第三象限

B.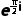为纯虚数

C.复数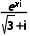的模等于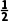

D.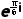的共轭复数为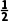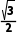－i

【迁移应用】

1.（2024·济南月考）欧拉公式e^iθ＝cos θ＋isin θ（e＝2.718 28…），被誉为数学上优美的数学公式.已知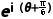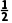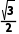＝＋i，则θ＝（）

A.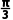＋2kπ（k∈Z）

B.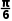＋2kπ（k∈Z）

C.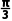＋kπ（k∈Z）

D.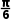＋kπ（k∈Z）

2.（多选）公式e^ix＝cos x＋isin x（x∈R，i为虚数单位）在复变函数中有非常重要的地位，被誉为“数学中的天桥”，据此公式，则有（）

A.e^iπ＋1＝0

B.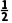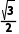（＋i）^{2 025}＝－1

C.｜e^ix＋e^－ix｜≤2

D.－2≤e^ix－e^－ix≤2

提示：完成课后作业第七章7.27.2.2