【免费下载】25-26学年同步培优讲义培优课 对称问题(学生版课时跟踪检测

培优课对称问题

1.已知点A（x，5）关于点（1，y）的对称点为（－2，－3），则点P（x，y）到原点的距离是（）

A.2B.4

C.5D.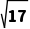

2.点P（2，5）关于x＋y＋1＝0的对称点的坐标为（）

A.（6，3）B.（3，－6）

C.（－6，－3）D.（－6，3）

3.（2024·周口质检）直线2x＋3y－6＝0关于点（1，－1）对称的直线方程是（）

A.3x－2y－6＝0B.2x＋3y＋7＝0

C.3x－2y－12＝0D.2x＋3y＋8＝0

4.两直线l₁：3x－2y－6＝0，l₂：3x－2y＋8＝0，则直线l₁关于直线l₂对称的直线方程为（）

A.3x－2y＋24＝0B.3x－2y－10＝0

C.3x－2y－20＝0D.3x－2y＋22＝0

5.（2024·阳江月考）如图所示，已知点A（4，0），B（0，4），从点P（2，0）射出的光线经直线AB反射后再射到直线OB上，最后经直线OB反射后又回到点P，则光线所经过的路程是（）

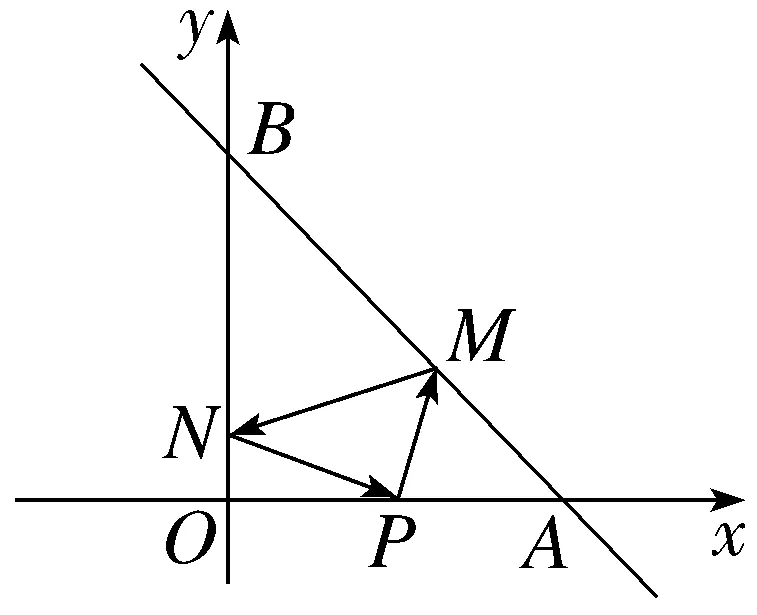
A.2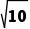B.6

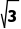C.3D.2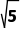

6.已知点A（－3，5），B（3，1），在直线l：y＝x上求一点P，使｜PA－PB｜的值最大，则P点的坐标为（）

A.（0，0）B.（）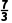

C.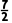（）D.（7，7）

7.（多选）已知直线l：y＝x，点A（0，－1），则（）

A.过点A与l平行的直线的方程为y＝x－1B.点A关于l对称的点的坐标为（0，1）

C.点A到直线l的距离为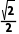D.过点A与l垂直的直线的方程为y＝－x－1

8.已知直线l：3x＋2y－1＝0与直线l₁关于直线x＋y＝0对称，则l₁的方程为.

9.已知入射光线经过点M（－3，4），被直线l：x－3＝0反射，反射光线经过点N（2，6），则反射光线所在直线的方程为.

10.（2024·南京质检）著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事休.”事实上，有很多代数问题可以转化为几何问题加以解决，如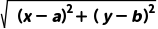：可以转化为平面上点M（x，y）与点N（a，b）的距离.结合上述观点，可得f（x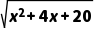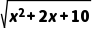）＝＋的最小值为.

11.若函数y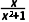＝的图象上存在两点P，Q关于点（1，0）对称，则直线PQ的方程是.

12.已知点M（3，5），在直线l：x－2y＋2＝0和y轴上各找一点P和Q，使△MPQ的周长最小，并求出P和Q两点的坐标.

13.已知直线l：x－y＋3＝0，一束光线从点A（1，2）处射向x轴上一点B，又从点B反射到l上的一点C，最后从点C反射回点A.

（1）试判断由此得到的△ABC的个数；

（2）求直线BC的方程.