

 互斥与独立事件关系的判断
互斥与独立事件关系的判断
1.互斥事件与独立事件的区别与联系
从互斥事件和独立事件的概念我们可以看出,互斥事件即互不相容,是不可能同时发生的事件,交集为空,但会产生相互影响(比如A发生,B就一定不发生了);独立事件A和B的发生互不影响,可能会同时发生.简单的说就是互斥必相互影响,独立必相容.
2.互斥事件与独立事件的运算性质
已知事件A,B发生的概率分别为P(A),P(B),则有
事件 | 表示 | 概率(A,B互斥) | 概率(A,B相互独立) |
A,B中至少有一个发生 | P(A∪B) | P(A)+P(B) | 1-P(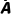 )P( )P(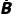 )或P(A)+P(B)-P(AB) )或P(A)+P(B)-P(AB) |
A,B都发生 | P(AB) | 0 | P(A)P(B) |
A,B都不发生 | P(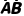 ) ) | 1-[P(A)+P(B)] | P(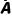 )P( )P(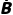 ) ) |
A,B恰有一个发生 | P(A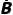 ∪ ∪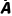 B) B) | P(A)+P(B) | P(A)P(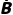 )+P( )+P(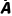 )P(B) )P(B) |
A,B中至多有一个发生 | P(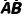 ∪A ∪A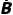 ∪ ∪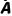 B) B) | 1 | 1-P(A)P(B) |
【例1】(2024·南阳月考)某社区举办“环保我参与”有奖问答比赛活动,某场比赛中,甲、乙、丙三个家庭同时回答一道有关环保知识的问题.已知甲家庭回答正确这道题的概率是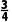 、丙两个家庭都回答错误的概率是
、丙两个家庭都回答错误的概率是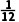 、丙两个家庭都回答正确的概率是
、丙两个家庭都回答正确的概率是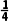 .若各家庭回答是否正确互不影响.
.若各家庭回答是否正确互不影响.
(1)求乙、丙两个家庭各自回答正确这道题的概率;
(2)求甲、乙、丙三个家庭中不少于2个家庭回答正确这道题的概率.
【例2】某服务电话,打进的电话响第1声时被接的概率是0.1;响第2声时被接的概率是0.2;响第3声时被接的概率是0.3;响第4声时被接的概率是0.35.
(1)打进的电话在响5声之前被接的概率是多少?
(2)打进的电话响4声而不被接的概率是多少?
提示:完成课后作业第十章10.2第1课时