

培优课解三角形中的综合问题
1.已知a,b,c分别是△ABC的内角A,B,C的对边,若△ABC的周长为4(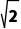 +1),且sin B+sin C=
+1),且sin B+sin C=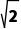 sin A,则a=()
sin A,则a=()
A.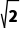 B.2
B.2
C.4D.2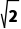
2.(2024·威海质检)在△ABC中,角A,B,C的对边分别为a,b,c,已知三个向量m=(a,cos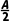 ),n=(b,cos
),n=(b,cos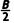 ),p=(c,cos
),p=(c,cos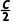 )共线,则△ABC为()
)共线,则△ABC为()
A.等边三角形B.钝角三角形
C.直角三角形D.等腰直角三角形
3.在△ABC中,角A,B,C的对边分别为a,b,c,已知△ABC的面积为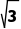 =120°,c=2bcos B,则AC边上的中线长为()
=120°,c=2bcos B,则AC边上的中线长为()
A.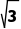 B.3C.
B.3C.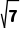 D.4
D.4
4.已知△ABC的内角A,B,C的对边分别为a,b,c,A=60°,b=3c,角A的平分线交BC于点D,且BD=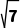 ∠ADB=()
∠ADB=()
A.-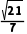 B.
B.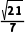 C.
C.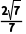 D.±
D.±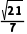
5.(2024·郑州月考)在△ABC中,角A,B,C的对边分别为a,b,c,且BC边上的高为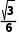 a,则
a,则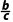 +
+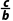 的最大值为()
的最大值为()
A.8B.6C.3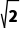 D.4
D.4
6.在△ABC中,角A,B,C所对的边分别为a,b,c,∠BAC=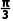 是BC上一点,且BD=3DC,AD=3,则△ABC面积的最大值是()
是BC上一点,且BD=3DC,AD=3,则△ABC面积的最大值是()
A.3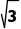 B.4
B.4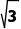 C.5
C.5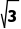 D.6
D.6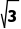
7.(多选)在Rt△ABC中,C=90°,角A的平分线交BC于点D,AD=1,cos∠BAC=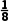 ()
()
A.AB=8B.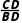 =
=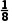
C.AB=6D.△ABD的面积为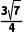
8.(多选)在△ABC中,内角A,B,C所对的边分别为a,b,c,且(a+b)∶(a+c)∶(b+c)=9∶10∶11,则下列结论正确的是()
A.sin A∶sin B∶sin C=4∶5∶6
B.△ABC是钝角三角形
C.△ABC的最大内角是最小内角的2倍
D.若c=6,则△ABC外接圆的半径为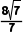
9.(2024·金华月考)在△ABC中,内角A,B,C所对的边分别为a,b,c,若2sin Asin Bcos C=sin2C,则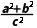 = ,角C的最大值为.
= ,角C的最大值为.
10.已知△ABC的内角A,B,C的对边分别为a,b,c.若C=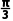 =6,1≤b≤4,则sin A的取值范围为.
=6,1≤b≤4,则sin A的取值范围为.
11.已知a=(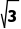 sin x,-cos x),b=(cos x,cos x),f(x)=a·b.
sin x,-cos x),b=(cos x,cos x),f(x)=a·b.
(1)求函数f(x)图象的对称轴方程;
(2)设△ABC的内角A,B,C所对的边分别为a,b,c,若f(B)=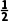 且b=
且b=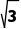 .求a+c的取值范围.
.求a+c的取值范围.
12.(2024·潮州月考)在△ABC中,D是BC上的点,AD平分∠BAC,△ABD的面积是△ADC面积的2倍.
(1)求 ;
;
(2)若AD=1,DC=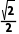 BD和AC的长.
BD和AC的长.
13.如图,某镇有一块空地形如△OAB,其中OA=3 km,OB=3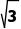 km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边AB上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.
km,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边AB上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为安全起见,需在△OAN的一周安装防护网.
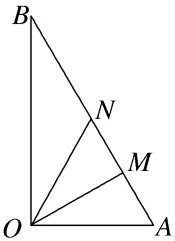
(1)当AM=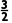 km时,求防护网的总长度;
km时,求防护网的总长度;
(2)为了节省投入的资金,人工湖△OMN的面积要尽可能小.问:如何设计施工方案,可使△OMN的面积最小,最小面积是多少?