 2022-2023学年度第二学期第一次月练习
2022-2023学年度第二学期第一次月练习
八年级数学
一、单选题(每题3分,共36分)
1. 下列二次根式中,是最简二次根式的是()
A. B. C. D.
2. 下列各组数中,不能作为直角三角形三边长度 是()
是()
A. 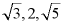 B. 3、4、5C.
B. 3、4、5C. 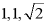 D. 9、12、15
D. 9、12、15
3. 若二次根式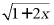 有意义,则x的取值范围为()
有意义,则x的取值范围为()
A. x≥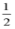 B. x≤-
B. x≤-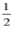 C. x≥-
C. x≥-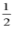 D. x≤
D. x≤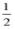
4. 下列性质中,平行四边形具有而非平行四边形不具有的是( )
A. 内角和为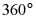 B. 外角和为
B. 外角和为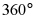
C. 对角线互相平分D. 对角互补
5. 如图,在平面直角坐标系中,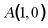 ,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,点C表示
,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,点C表示 实数介于()
实数介于()
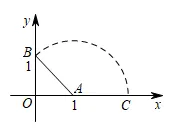
A. 1到2之间B. 2到3之间C. 3到4之间D. 4到5之间
6. 实数a,b在数轴上的位置如图所示,且|a|>|b|,则化简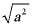 ﹣|2a+b|的结果为( )
﹣|2a+b|的结果为( )
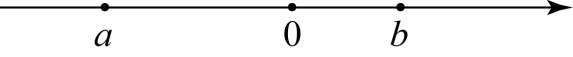
A. 2a+bB. ﹣2a+bC. a+bD. 2a﹣b
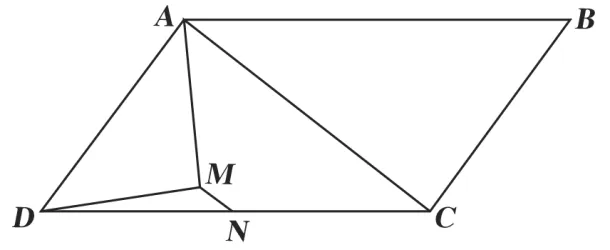
7. 如图,▱ABCD中,CD=4,BC=6,按以下步骤作图:①以点C为圆心,适当长度为半径作弧,分别交BC,CD于M,N两点:②分别以点M,N为圆心,以大于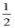 MN的长为半径画弧,两弧在▱ABCD的内部交于点P;③连接CP并延长交AD于点E,交BA的延长线于点F,则AF的长为( )
MN的长为半径画弧,两弧在▱ABCD的内部交于点P;③连接CP并延长交AD于点E,交BA的延长线于点F,则AF的长为( )
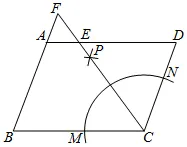
A. 1B. 2C. 2.5D. 3
8. △ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是( )
A. ∠A:∠B:∠C=1:2:3
B. 三边长为a,b,c 值为1,2,
值为1,2,
C. 三边长为a,b,c的值为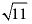
D. 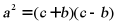
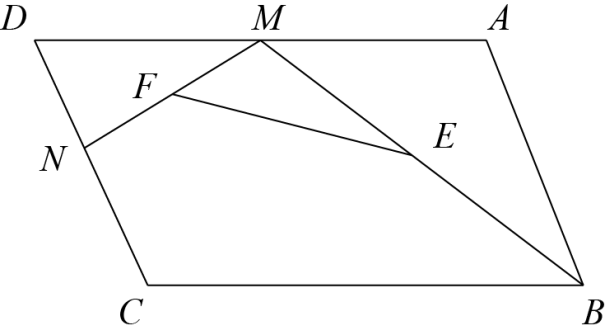
9. 如图,已知平行四边形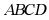 中,M,N分别是
中,M,N分别是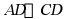 上
上 点,E,F分别是
点,E,F分别是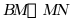 的中点,当M在
的中点,当M在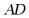 上从A向D移动而N不动时,那么下列结论成立的是()
上从A向D移动而N不动时,那么下列结论成立的是()
A. 线段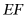 的长逐渐增大B. 线段的长逐渐减小
的长逐渐增大B. 线段的长逐渐减小
C. 线段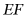 的长不改变D. 线段
的长不改变D. 线段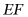 的长不能确定
的长不能确定
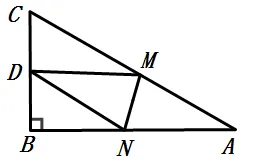
10. 如图,Rt△ABC中,AB=9,BC=6,∠B=90˚,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A. 6B. 5C. 4D. 3
11. 如图,在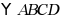 中,AC与BD交于点M,点F在AD上,
中,AC与BD交于点M,点F在AD上,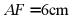 ,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动()秒时,以P、Q、E、F为顶点的四边形是平行四边形.
,点E是BC的中点,若点P以1cm/秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动()秒时,以P、Q、E、F为顶点的四边形是平行四边形.
A. 3B. 3或5C. 5D. 4或5
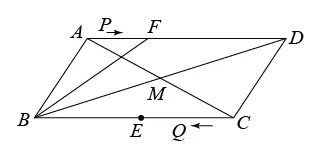
12. 如图,在平行四边形ABCD中,对角线AC⊥BC,M在∠CAD的平分线上,且AM⊥DM,点N为CD的中点,连接MN,若AD=12,MN=2.则AB的长为( )
A. 12B. 20C. 24D. 30
二、填空题(每题3分,共18分)
13. 若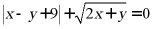 ,则x+y=_____.
,则x+y=_____.
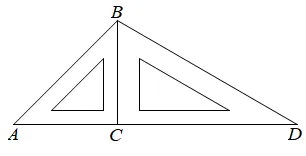
14. 如图,把含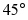 角的两块直角三角形放置在同一平面内,若
角的两块直角三角形放置在同一平面内,若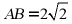 ,则
,则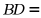 _____.
_____.
15. 已知四边形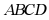 ,有下列条件:①
,有下列条件:①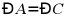 ;②
;②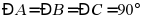 ;③
;③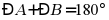 ;④
;④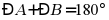 .其中能判定四边形
.其中能判定四边形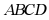 是平行四边形的是_______(填序号)
是平行四边形的是_______(填序号)
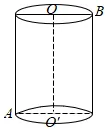
16. 如图,圆柱的底面半径为24,高为7π,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是_____.
17. 在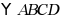 中,
中,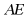 平分
平分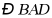 交
交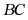 边于点
边于点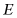 平分
平分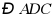 交
交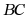 边于点
边于点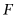 ,若
,若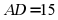 ,则
,则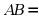 _________.
_________.
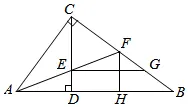
18. 如图,直角三角形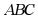 中,
中,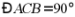 于点
于点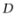 平分
平分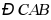 交
交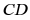 于点
于点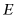 ,交
,交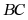 于点
于点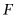 交
交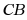 于点
于点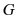 于
于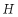 ,以下4个结论:①
,以下4个结论:①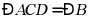 ;②
;②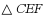 是等边三角形;③
是等边三角形;③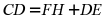 ;④
;④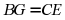 中正确的是______(将正确结论的序号填空)
中正确的是______(将正确结论的序号填空)
三、解答题(共66分)
19. 计算:
(1)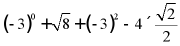
(2)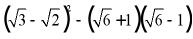
20. 在Rt△ABC中,∠C=90°
①若a=40,c=41,则b=;
②若c=13,b=5,则a=;
③已知a:b=3:4,c=15,则a=;b=.
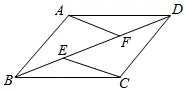
21. 如图,在平行四边形ABCD中,E、F为对角线BD上的两点,且∠BAF=∠DCE.求证:BE=DF.
22. 如图,在正方形网格中,小正方形的边长为1,点A,B,C为网格的交点.
(1)判断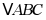 的形状,并说明理由;
的形状,并说明理由;
(2)求AB边上的高.
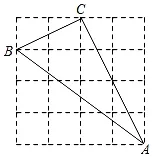
23. 已知:如图,四边形ABCD中,AB⊥BC,AB=1,BC=2,CD=2,AD=3,
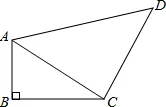
(1)求AC的长;
(2)求证:△ACD是直角三角形;
(3)四边形ABCD的面积.
24. 如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD 中点,连接BE并延长至点
中点,连接BE并延长至点


通过网盘分享的文件:【免费下载】精编天津市东丽区英华学校20222023学年八年级下学期第一次月考数学试卷
链接: https://pan.baidu.com/s/18x37rl_KwFFLlcX8gw4nQQ?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享