,故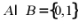 ,
,
故选:D.
4.C
【分析】移项后转化为求一元二次不等式的解即可.
【详解】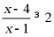 即为
即为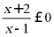 即
即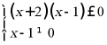 ,故
,故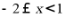 ,
,
故解集为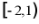 ,
,
故选:C.
5.A
【分析】由余弦定理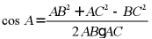 直接计算求解即可.
直接计算求解即可.
【详解】由题意得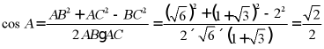 ,
,
又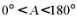 ,所以
,所以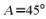 .
.
故选:A
6.C
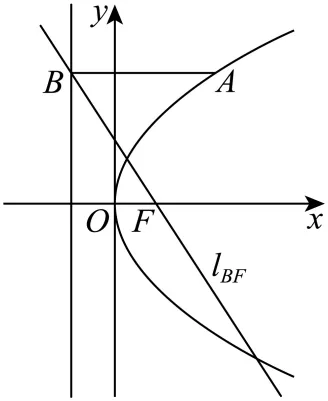
【分析】先由直线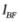 求出焦点
求出焦点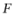 和
和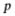 即抛物线
即抛物线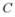 的方程,进而依次得抛物线的准线方程和点B,从而可依次求出
的方程,进而依次得抛物线的准线方程和点B,从而可依次求出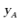 和
和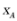 ,再由焦半径公式即可得解.
,再由焦半径公式即可得解.
【详解】对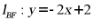 ,令
,令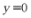 ,则
,则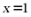 ,
,
所以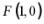 即抛物线
即抛物线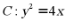 ,故抛物线的准线方程为
,故抛物线的准线方程为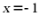 ,
,
故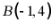 ,则
,则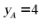 ,代入抛物线
,代入抛物线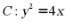 得
得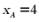 .
.
所以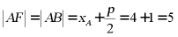 .
.
故选:C
7.B
【分析】由等差数列前n项和公式结合题意列出关于首项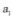 和公差d的方程求出首项
和公差d的方程求出首项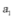 和公差d,再由等差数列前n项和公式
和公差d,再由等差数列前n项和公式


通过网盘分享的文件:【免费下载】高考真题【吉林】2025年高考全国二卷数学高考真题解析word版含解析学生版教师版
链接: https://pan.baidu.com/s/1PllAmw63n04AmdLKaXyolg?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享