【免费下载】25-26学年同步培优讲义第3课时 利用导数解决与函数有关的问题(学生版

第3课时利用导数解决与函数有关的问题

【例1】已知f（x）＝（a－x＋1）e^x，其中a＞0，试画出函数f（x）的大致图象.

通性通法

利用导数画函数大致图象的步骤

（1）确定函数的定义域；

（2）利用导数确定函数的单调性与极值；

（3）确定f（x）的图象经过一些特殊点，以及图象的变化趋势；

（4）画出f（x）的大致图象.

【跟踪训练】

试画出函数f（x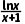）＝的图象.

【例2】判断函数f（x）＝e^x（x²－2x＋1）－x的零点个数.

通性通法

利用导数确定函数零点或方程根的个数的方法

（1）数形结合：将函数的零点或方程的根转化为两函数图象的交点，利用导数画出函数的大致图象，进而得到函数零点的个数；

（2）利用零点存在定理：先用该定理判断函数在某区间上有零点，然后利用导数研究函数的单调性、极值和区间端点处的函数值的符号，进而判断函数在该区间上的零点个数.

【跟踪训练】

（2024·郑州月考）若函数f（x）＝ax³－bx＋4，当x＝2时，函数f（x）取得极值－.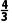

（1）求函数f（x）的解析式；

（2）若方程f（x）＝k有3个不同的实数根，求实数k的取值范围.

【例3】（2024·宁波月考）某小型电子产品厂经过市场调研，生产某小型电子产品需要年投入固定成本2万元，每生产x万件，需另投入流动成本W（x）万元，在年产量不足4万件时，W（x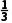）＝x³＋2x；在年产量不小于4万件时，W（x）＝7x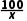＋－27.每件产品售价6元.通过市场分析，生产的商品当年能全部售完.

（1）写出年利润P（x）（万元）关于年产量x（万件）的函数解析式；（年利润＝年销售收入－固定成本－流动成本）

（2）年产量为多少万件时，在这一商品的生产中所获利润最大？最大利润是多少？

通性通法

1.利用导数解决实际问题时，要注意以下几点

（1）当问题中涉及多个变量时，应根据题意分析它们的关系，找出变量间的关系式；

（2）确定函数关系式中自变量的取值范围；

（3）所得的结果要符合问题的实际意义.

2.要注意方法的灵活运用，如配方法、基本不等式法等.

【跟踪训练】

某村庄拟修建一个无盖的圆柱形蓄水池（不计厚度）.设该蓄水池的底面半径为r米，高为h米，体积为V立方米.假设建造成本仅与表面积有关，侧面的建造成本为100元/平方米，底面的建造成本为160元/平方米，该蓄水池的总建造成本为12 000π元（π为圆周率）.

（1）将V表示成r的函数V（r），并求该函数的定义域；

（2）讨论函数V（r）的单调性，并确定r和h为何值时该蓄水池的体积最大.

1.已知某生产厂家的年利润y（单位：万元）与年产量x（单位：万件）的函数关系式为y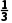＝－x³＋81x－234，则使该生产厂家获得最大年利润的年产量为（）

A.13万件B.11万件

C.9万件D.7万件

2.（2024·揭阳月考）函数f（x）＝（x－1）e^x的图象大致为（）

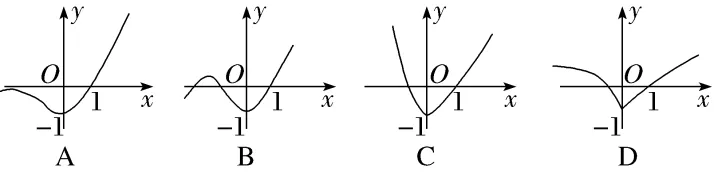
3.已知函数f（x）＝（x²＋a）e^x有最小值，则函数y＝f'（x）的零点个数为（）

A.0B.1

C.2D.不确定

提示：完成课后作业第五章5.35.3.2第3课时