

2.5 直线与圆、圆与圆的位置关系
2.5.1 直线与圆的位置关系
新课程标准解读 | 核心素养 |
1.能根据给定直线、圆的方程,判断直线与圆的位置关系 | 逻辑推理、 直观想象 |
2.能用直线和圆的方程解决一些简单的问题.体会用代数方法处理几何问题的思想 | 直观想象、 数学运算 |
第1课时直线与圆的位置关系


“大漠孤烟直,长河落日圆”是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象.如果我们把太阳看成一个圆,地平线看成一条直线,观察下面三幅太阳落山的图片.
【问题】(1)图片中,地平线与太阳有怎样的位置关系?
(2)上述直线与圆的位置关系,怎样用代数方法表示?

知识点直线与圆的位置关系
1.直线与圆的三种位置关系
位置关系 | 交点个数 | 图示 |
相交 | 有 两个 公共点 | 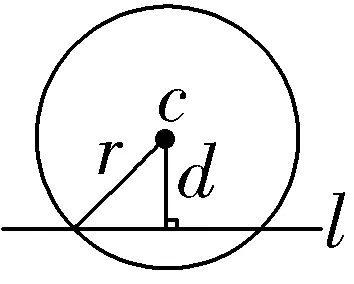
|
相切 | 只有 一个 公共点 | 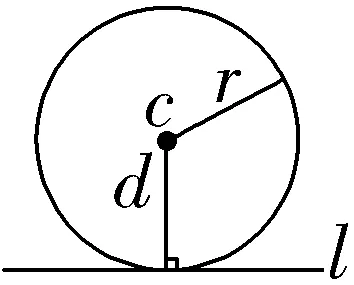
|
相离 | 没有 公共点 | 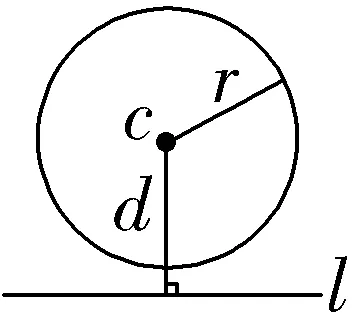
|
2.直线与圆的位置关系的判断
位置关系 | 相交 | 相切 | 相离 |
判断方法 | 几何法:设圆心到直线的距离d=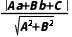 | d<r | d=r | d>r |
代数法:由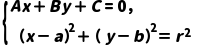 消元得到一元二次方程的判别式Δ | Δ>0 | Δ=0 | Δ<0 |
【想一想】
1.若直线与圆只有一个公共点,则直线与圆一定相切吗?
提示:一定.
2.若直线与圆有公共点,则圆心到直线的距离满足什么条件?
提示:当直线与圆有公共点时,圆心到直线的距离小于或等于半径.

1.判断正误.(正确的画“√”,错误的画“×”)
(1)若直线与圆有公共点,则直线与圆相交.(×)
(2)如果直线与圆组成的方程组有解,则直线和圆相交或相切.(√)
(3)若圆心到直线的距离大于半径,则直线与圆的方程联立消元后得到的一元二次方程无解.(√)
(4)过圆外一点的直线与圆相离.(×)
2.直线y=x+1与圆x2+y2=1的位置关系为()
A.相切B.相交但直线不过圆心
C.直线过圆心D.相离
解析:B圆心(0,0)到直线y=x+1的距离d=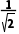 =
=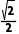 .因为0<
.因为0<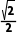 <1,所以直线与圆相交但直线不过圆心,故选B.
<1,所以直线与圆相交但直线不过圆心,故选B.
3.直线x+y+m=0与圆x2+y2=m相切,则m的值为()
A.0或2B.2
C.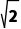 D.无解
D.无解
解析:B由于直线与圆相切,故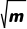 =
=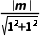 m=0(舍去)或m=2.
m=0(舍去)或m=2.
4.圆(x-1)2+(y+4)2=25在x轴截得的弦长是()
A.8B.6
C.5D.6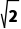
解析:B令y=0,得(x-1)2=9,所以x-1=±3,所以x1=-2,x2=4,故所求弦长为|x1-x2|=6.故选B.

【例1】(2024·滨州月考)若直线4x-3y+a=0与圆x2+y2=100有如下关系:①相交;②相切;③相离.试分别求实数a的取值范围.
解:法一(代数法)由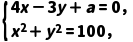 消去y,得25x2+8ax+a2-900=0,
消去y,得25x2+8ax+a2-900=0,
Δ=(8a)2-4×25(a2-900)=-36a2+90 000.
①当直线和圆相交时,Δ>0,即-36a2+90 000>0,解得-50<a<50.
②当直线和圆相切时,Δ=0,即a=50或a=-50.
③当直线和圆相离时,Δ<0,即a<-50或a>50.
法二(几何法)圆x2+y2=100的圆心为(0,0),半径r=10,
则圆心到直线的距离d=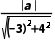 =
=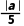 .
.
①当直线和圆相交时,d<r,
即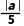 <10,-50<a<50.
<10,-50<a<50.
②当直线和圆相切时,d=r,
即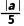 =10,a=50或a=-50.
=10,a=50或a=-50.
③当直线和圆相离时,d>r,
即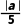 >10,a<-50或a>50.
>10,a<-50或a>50.
通性通法
直线与圆的位置关系的判断方法
(1)几何法:利用圆心到直线的距离d和圆的半径r的大小关系.d<r⇔相交;d=r⇔相切;d>r⇔相离.
(2)代数法:Δ=b2-4ac
【跟踪训练】
1.已知圆C:x2+y2-4x=0,l是过点P(3,0)的直线,则()
A.l与C相交B.l与C相切
C.l与C相离D.以上三个选项均有可能
解析:A将点P(3,0)代入圆的方程,得32+02-4×3=9-12=-3<0,∴点P(3,0)在圆内.∴过点P的直线l必与圆C相交.
2.若直线x-y+1=0与圆(x-a)2+(y-1)2=2没有公共点,则实数a的取值范围是()
A.(-∞,-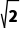 )∪(
)∪(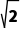 ,+∞)
,+∞)
B.(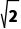 ,+∞)
,+∞)
C.(-∞,-2)∪(2,+∞)
D.(2,+∞)
解析:C由题意得圆心坐标为(a,1),半径为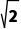
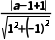 >
>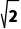 a|>2,∴a>2或a<-2.∴实数a的取值范围是(-∞,-2)∪(2,+∞).
a|>2,∴a>2或a<-2.∴实数a的取值范围是(-∞,-2)∪(2,+∞).
【例2】(2024·福州月考)过点M(2,4)向圆(x-1)2+(y+3)2=1引切线,求其切线方程.
解:由于(2-1)2+(4+3)2=50>1,故点M在圆外.
当切线斜率存在时,设切线方程是y-4=k(x-2),
即kx-y+4-2k=0,
由于直线与圆相切,圆心为(1,-3),r=1,故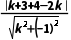 =1,解得k=
=1,解得k=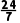 .
.
所以切线方程为24x-7y-20=0.
又当切线斜率不存在时,直线x=2与圆相切.
综上所述,所求切线方程为24x-7y-20=0或x=2.
【母题探究】
1.(变条件)若将本例中的点M的坐标改为(1,-2),其他条件不变,又如何求其切线方程?
解:由于(1-1)2+(-2+3)2=1,
故点M在圆上,
设圆的圆心为C,则C(1,-3),显然CM的斜率不存在.
因为圆的切线垂直于经过切点的半径,
所以所求切线的斜率k=0,
所以切线方程为y=-2.
2.(变设问)若本例中的条件不变,如何求其切线长?
解:由题知,设切线长为d,
d=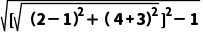
=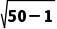 =7.
=7.
通性通法
1.过圆上一点(x0,y0)的圆的切线方程的求法
先求切点与圆心连线的斜率k,再由垂直关系得切线的斜率为-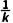 .如果切线斜率为零或不存在,则由图形可直接得切线方程y=y0或x=x0.
.如果切线斜率为零或不存在,则由图形可直接得切线方程y=y0或x=x0.
2.过圆外一点(x0,y0)的圆的切线方程的求法
设切线方程为y-y0=k(x-x0),由圆心到直线的距离等于半径建立方程,可求得k,也就得切线方程.当用此法只求出一个方程时,另一个方程应为x=x0,因为在上面解法中不包括斜率不存在的情况,而过圆外一点的切线有两条.
3.求切线长(最值)的两种方法
(1)代数法:直接利用勾股定理求出切线长,把切线长中的变量统一成一个,转化成函数求最值;
(2)几何法:把切线长最值问题转化成圆心到直线的距离问题.
【跟踪训练】
1.若直线x-y+2=0与圆O:(x-a)2+y2=2相切,则a=()
A.0B.-4或2
C.2D.0或-4
解析:D由圆O:(x-a)2+y2=2可得圆心O(a,0),半径r=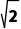 x-y+2=0与圆O:(x-a)2+y2=2相切,所以圆心O(a,0)到直线x-y+2=0的距离d=
x-y+2=0与圆O:(x-a)2+y2=2相切,所以圆心O(a,0)到直线x-y+2=0的距离d=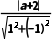 =
=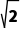 |a+2|=2,所以a=0或a=-4,故选D.
|a+2|=2,所以a=0或a=-4,故选D.
2.由直线y=x+1上任一点向圆(x-3)2+y2=1引切线,则该切线长的最小值为()
A.1B.2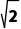
C.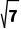 D.3
D.3
解析:C圆心C(3,0)到y=x+1的距离d=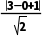 =2
=2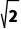 .所以切线长的最小值为l=
.所以切线长的最小值为l=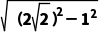 =
=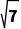 .
.
【例3】过圆x2+y2=8内的点P(-1,2)作直线l交圆于A,B两点,若直线l的倾斜角为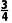 π,求弦AB的长.
π,求弦AB的长.
解:法一设A(x1,y1),B(x2,y2).由题意知直线l的方程为y-2=-(x+1),即x+y-1=0.
由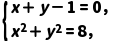 消去y,得2x2-2x-7=0,所以x1+x2=1,x1x2=-
消去y,得2x2-2x-7=0,所以x1+x2=1,x1x2=-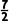
所以|AB|=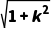 |x1-x2|=
|x1-x2|=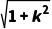 ·
·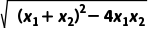 =
=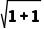 ·
·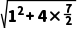 =
=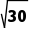 (k为直线l的斜率).
(k为直线l的斜率).
法二由题意知直线l的方程为y-2=-(x+1),即x+y-1=0.
圆心(0,0)到直线l的距离d=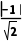 =
=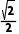
则有|AB|=2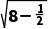 =
=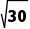 .
.
通性通法
求弦长常用的3种方法
(1)利用圆的半径r,圆心到直线的距离d,弦长l之间的关系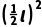 +d2=r2解题;
+d2=r2解题;
(2)利用交点坐标,若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间距离公式计算弦长;
(3)利用弦长公式,设直线l:y=kx+b,与圆的两交点(x1,y1),(x2,y2),将直线方程代入圆的方程,消元后利用根与系数的关系得弦长l=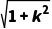 |x1-x2|=
|x1-x2|=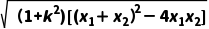 .
.
【跟踪训练】
1.(2024·丽水质检)若点P(2,-1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程是()
A.2x-y-5=0B.2x+y-3=0
C.x+y-1=0D.x-y-3=0
解析:D∵AB是圆(x-1)2+y2=25的弦,圆心为C(1,0),AB的中点P(2,-1)满足AB⊥CP,∴AB的斜率k=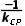 =
=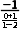 =1,可得直线AB的方程为y+1=x-2,化简得x-y-3=0,故选D.
=1,可得直线AB的方程为y+1=x-2,化简得x-y-3=0,故选D.
2.若直线x-y=2被圆(x-a)2+y2=4所截得的弦长为2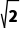 a的值为.
a的值为.
答案:0或4
解析:由圆的方程,可知圆心坐标为(a,0),半径r=2.又直线被圆截得的弦长为2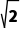 d=
d=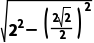 =
=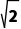 .又d=
.又d=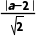 |a-2|=2,解得a=4或a=0.
|a-2|=2,解得a=4或a=0.

1.(2024·河源月考)若直线x-y=0与圆(x-1)2+(y+1)2=m相离,则实数m的取值范围是()
A.(0,2]B.(1,2]
C.(0,2)D.(1,2)
解析:C由题意得圆心到直线的距离为d=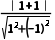 >
>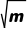 m<2.∵m>0,∴0<m<2.故选C.
m<2.∵m>0,∴0<m<2.故选C.
2.(多选)若直线3x+4y=b与圆x2+y2-2x-2y+1=0相切,则b=()
A.-2B.-12
C.2D.12
解析:CD圆的方程为x2+y2-2x-2y+1=0,可化为(x-1)2+(y-1)2=1,由圆心(1,1)到直线3x+4y-b=0的距离为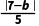 =1,得b=2或12.
=1,得b=2或12.
3.若圆C的圆心为(3,0),直线l:x-y-1=0被该圆所截得的弦长为2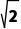 C的标准方程.
C的标准方程.
解:设圆的半径为r,依题意,圆心(3,0)到直线x-y-1=0的距离为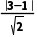 =
=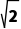
则由垂径定理得r2=(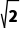 )2+(
)2+(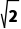 )2=4,∴r=2,
)2=4,∴r=2,
∴圆的标准方程为(x-3)2+y2=4.
 圆的切线与切点弦
圆的切线与切点弦
若P0(x0,y0)是圆O:x2+y2=r2上一点,则圆O的过点P0的切线方程是x0x+y0y=r2.事实上,因为点P0(x0,y0)在圆O:x2+y2=r2上,所以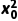 +
+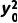 =r2,即x0·x0+y0·y0=r2,从而点P0在直线x0x+y0y=r2上.又因为圆心O到直线x0x+y0y=r2的距离d=
=r2,即x0·x0+y0·y0=r2,从而点P0在直线x0x+y0y=r2上.又因为圆心O到直线x0x+y0y=r2的距离d=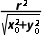 =r,所以x0x+y0y=r2是圆O的过点P0的切线方程.
=r,所以x0x+y0y=r2是圆O的过点P0的切线方程.
【问题探究】
当点P0(x0,y0)在圆O外时,方程x0x+y0y=r2表示怎样的直线呢?
提示:如图,过P0(x0,y0)作圆O的两条切线,切点分别为A,B.
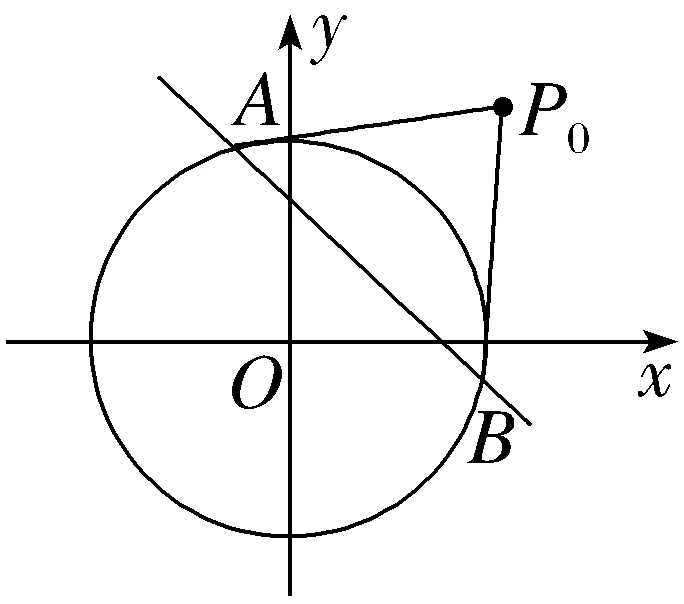
设A(x1,y1),B(x2,y2),则直线P0A的方程为x1x+y1y=r2.
因为P0(x0,y0)在直线P0A上,所以x1x0+y1y0=r2,
故(x1,y1)满足方程x0x+y0y=r2,
即点A在直线x0x+y0y=r2上.
同理点B在直线x0x+y0y=r2上.
所以x0x+y0y=r2是直线AB的方程,即切点弦所在直线的方程.
【迁移应用】
当点P0(x0,y0)在圆O内(异于点O)时,方程x0x+y0y=r2表示怎样的直线?
解:圆心O(0,0)到直线x0x+y0y=r2的距离d=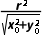 点P0(x0,y0)在圆O内,即
点P0(x0,y0)在圆O内,即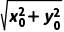 <r,
<r,
则d>r,故直线与圆相离.


1.直线y=ax+1与圆x2+y2-2x-3=0的位置关系是()
A.相切B.相交
C.相离D.随a的变化而变化
解析:B∵直线y=ax+1恒过定点(0,1),且点(0,1)在圆x2+y2-2x-3=0的内部,∴直线与圆相交.
2.直线x+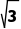 y+12=0被圆x2+y2=100所截得的弦长为()
y+12=0被圆x2+y2=100所截得的弦长为()
A.2B.4
C.8D.16
解析:D圆x2+y2=100的圆心坐标为(0,0),半径为10,圆心(0,0)到直线x+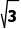 y+12=0的距离d=
y+12=0的距离d=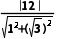 =6,则直线x+
=6,则直线x+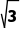 y+12=0被圆x2+y2=100所截得的弦长为2
y+12=0被圆x2+y2=100所截得的弦长为2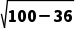 =16.故选D.
=16.故选D.
3.圆心为(3,0)且与直线x+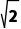 y=0相切的圆的方程为()
y=0相切的圆的方程为()
A.(x-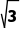 )2+y2=1B.(x-3)2+y2=3
)2+y2=1B.(x-3)2+y2=3
C.(x-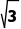 )2+y2=3D.(x-3)2+y2=9
)2+y2=3D.(x-3)2+y2=9
解析:B由题意知所求圆的半径r=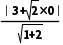 =
=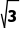 (x-3)2+y2=3,故选B.
(x-3)2+y2=3,故选B.
4.直线l与圆x2+y2+2x-4y+a=0(a<3)相交于A,B两点,若弦AB的中点为C(-2,3),则直线l的方程为()
A.x-y+5=0B.x+y-1=0
C.x-y-5=0D.x+y-3=0
解析:A由圆的一般方程可得圆心为M(-1,2).由圆的性质易知M(-1,2)与C(-2,3)的连线与弦AB垂直,故有kAB×kMC=-1⇒kAB=1,故直线AB的方程为y-3=x+2,整理得x-y+5=0.
5.(多选)(2024·汕尾月考)给定直线l:3x+4y=0和圆C:x2-4x+y2=m-5,则()
A.实数m的取值范围为(0,+∞)
B.当l与圆C相切时,m=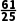
C.当1<m<2时,l与圆C相离
D.当l与圆C相交时,m>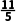
解析:BC圆C:x2-4x+y2=m-5的标准方程为(x-2)2+y2=m-1,圆心为C(2,0),半径r=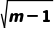 .对于A:由r=
.对于A:由r=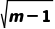 >0,解得m>1,故A错误;对于B:因为C(2,0)到直线l:3x+4y=0的距离d=
>0,解得m>1,故A错误;对于B:因为C(2,0)到直线l:3x+4y=0的距离d=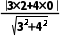 =
=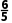 l与圆C相切时,r=
l与圆C相切时,r=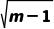 =
=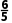 m=
m=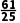 B正确;对于C:当1<m<2时,0<r<1<
B正确;对于C:当1<m<2时,0<r<1<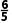 l与圆C相离,故C正确;对于D:当l与圆C相交时,>
l与圆C相离,故C正确;对于D:当l与圆C相交时,>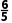 m>
m>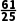 D错误.故选B、C.
D错误.故选B、C.
6.(多选)与圆C:x2+y2-4x+2=0相切,且在x,y轴上的截距相等的直线方程为()
A.x+y=0B.x-y=0
C.x=0D.x+y=4
解析:ABD圆C的方程可化为(x-2)2+y2=2.可分为两种情况讨论:
①直线在x,y轴上的截距均为0,易知直线斜率必存在,设直线方程为y=kx,则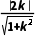 =
=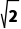 k=±1,所以直线方程为y=±x;
k=±1,所以直线方程为y=±x;
②直线在x,y轴上的截距均不为0,则可设直线方程为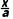 +
+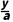 =1(a≠0),即x+y-a=0(a≠0),则
=1(a≠0),即x+y-a=0(a≠0),则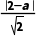 =
=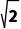 a=4(a=0舍去),所以直线方程为x+y-4=0.
a=4(a=0舍去),所以直线方程为x+y-4=0.
7.若点P(1,2)在以坐标原点为圆心的圆上,则该圆在点P处的切线方程为x+2y-5=0.
解析:设切线斜率为k,则由已知得k·kOP=-1.
∴k=-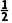 .∴切线方程为x+2y-5=0.
.∴切线方程为x+2y-5=0.
8.(2024·苏州月考)由直线y=x+1上的点向圆(x-3)2+y2=1作切线,则切线长的最小值为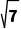 .
.
解析:切线长的最小值是当直线y=x+1上的点与圆心距离最小时取得,易知圆心(3,0)到直线的距离d=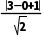 =2
=2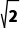 r=1,所以切线长的最小值为
r=1,所以切线长的最小值为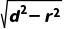 =
=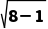 =
=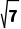 .
.
9.一条光线从点(-2,-3)射出,经y轴反射后与圆(x+3)2+(y-2)2=1相切,则反射光线所在直线的斜率为-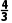 或-
或-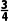 .
.
解析:由已知得点(-2,-3)关于y轴的对称点为(2,-3),由入射光线与反射光线的对称性知,反射光线一定过点(2,-3).设反射光线所在直线的斜率为k,则反射光线所在直线的方程为y+3=k(x-2),即kx-y-2k-3=0.由反射光线与圆相切,则有d=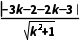 =1,解得k=-
=1,解得k=-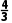 或k=-
或k=-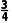 .
.
10.已知直线l:2x+y-4=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆C的位置关系;如果相交,求出它们的交点坐标.
解:由直线l和圆的方程,得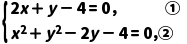
消去y,得5x2-12x+4=0.
∵Δ=(-12)2-4×5×4=64>0,
∴直线l与圆C相交,有两个公共点.
由5x2-12x+4=0,得x1=2,x2=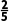 .
.
把x1=2代入方程①,得y1=0;把x2=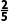 代入方程①,得y2=
代入方程①,得y2=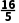 .
.
∴直线l与圆相交,有两个公共点,它们的坐标分别是(2,0)和(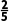 ).
).

11.已知直线2x+my-8=0与圆C:(x-m)2+y2=4相交于A,B两点,且△ABC为等腰直角三角形,则实数m=()
A.2B.14
C.2或14D.1
解析:C由题意知圆C的半径r=2,则有|AC|=|BC|=2.因为△ABC为等腰直角三角形,则圆心(m,0)到直线的距离d=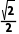 r=
r=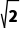 d=
d=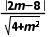 =
=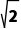 m=14或m=2.故选C.
m=14或m=2.故选C.
12.(2024·济宁质检)直线y=x+b与曲线x=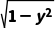 有且只有一个交点,则b满足()
有且只有一个交点,则b满足()
A.|b|=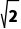 B.-1<b≤1或b=-
B.-1<b≤1或b=-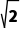
C.-1≤b<1D.非以上答案
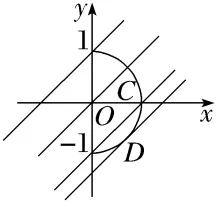
解析:B曲线x=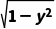 含有限制条件,即x≥0,故曲线并非表示整个单位圆,仅仅是单位圆在y轴右侧(含与y轴的交点)的部分.在同一平面直角坐标系中,画出y=x+b与曲线x=
含有限制条件,即x≥0,故曲线并非表示整个单位圆,仅仅是单位圆在y轴右侧(含与y轴的交点)的部分.在同一平面直角坐标系中,画出y=x+b与曲线x=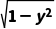 (即x2+y2=1,x≥0)的图象,如图所示.当直线与曲线相切时,b=-
(即x2+y2=1,x≥0)的图象,如图所示.当直线与曲线相切时,b=-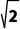 -1<b≤1.
-1<b≤1.
13.(多选)已知圆C:x2+y2-6x-8y+21=0和直线l:kx-y+3-4k=0,则()
A.直线l与圆C的位置关系无法判定
B.当k=1时,圆C上的点到直线l的最远距离为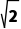 +2
+2
C.当圆C上有且仅有3个点到直线l的距离等于1时,k=0
D.若直线l与圆C交于M,N两点,则MN的中点的轨迹是一个圆
解析:BCD由x2+y2-6x-8y+21=0,得(x-3)2+(y-4)2=4,所以圆心C的坐标为(3,4),半径为2.由直线l的方程可得y-3=k(x-4),则直线l恒过定点(4,3),此点在圆C内,故直线l与圆C相交.故A错误;当k=1时,直线l的方程为x-y-1=0.设圆心C(3,4)到直线l的距离为d,则d=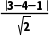 =
=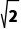 C上的点到直线l的最远距离为
C上的点到直线l的最远距离为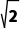 +2.故B正确;当圆C上有且仅有3个点到直线l的距离等于1时,圆心C(3,4)到直线l的距离为1,由
+2.故B正确;当圆C上有且仅有3个点到直线l的距离等于1时,圆心C(3,4)到直线l的距离为1,由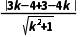 =1,得k=0.故C正确;设直线l恒过的定点为A,MN的中点为P,由垂径定理知PC⊥PA,故点P的轨迹是以AC为直径的圆,故D正确.故选B、C、D.
=1,得k=0.故C正确;设直线l恒过的定点为A,MN的中点为P,由垂径定理知PC⊥PA,故点P的轨迹是以AC为直径的圆,故D正确.故选B、C、D.
14.已知圆C过点(1,1),圆心在x轴正半轴上,且与直线y=x-4相切.
(1)求圆C的标准方程;
(2)已知过点P(1,3)的直线l交圆C于A,B两点,且|AB|=2,求直线l的方程.
解:(1)由题意,设圆心坐标为C(a,0)(a>0),
由题意,得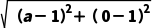 =
=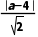
解得a=-6(舍)或a=2,
所以圆的半径为r=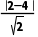 =
=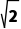
则圆C的标准方程为(x-2)2+y2=2.
(2)若斜率不存在,则直线方程为x=1,弦心距d=1,半径为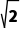
则|AB|=2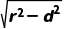 =2,符合题意;
=2,符合题意;
若斜率存在,设直线方程为y-3=k(x-1),
即kx-y-k+3=0.
弦心距d=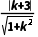 |AB|=2
|AB|=2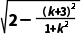 =2,
=2,
解得k=-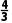 4x+3y-13=0.
4x+3y-13=0.
综上所述,直线l的方程为x=1或4x+3y-13=0.

15.(2024·淮安月考)几何学史上有一个著名的米勒问题:“设点M,N是锐角∠AQB的边QA上的两点,试在边QB上找一点P,使得∠MPN最大”.如图,其结论是:点P为过M,N两点且和射线QB相切的圆与射线QB的切点.根据该结论解决以下问题:在平面直角坐标系中,给定两点M(-1,2),N(1,4),点P在x轴上移动,当∠MPN取最大值时,点P的横坐标是1.
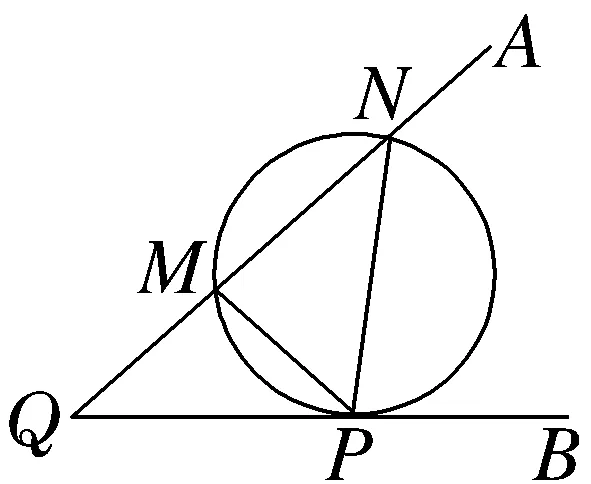
解析:∵点M(-1,2),N(1,4),则线段MN的中点坐标为(0,3),易知kMN=1,则经过M,N两点的圆的圆心在线段MN的垂直平分线y=3-x上,设圆心为S(a,3-a),则圆S的方程为(x-a)2+(y-3+a)2=2(1+a2),由题中结论得,当∠MPN取最大值时,圆S必与x轴相切于点P,则此时点P的坐标为(a,0),代入圆S的方程得2(1+a2)=(a-3)2,解得a=1或a=-7,即对应的切点分别为P(1,0)和P'(-7,0),对于定长的弦在弧上所对的圆周角会随着圆的半径减小而角度增大,又过点M,N,P'的圆的半径大于过点M,N,P的圆的半径,∴∠MPN>∠MP'N,故点P(1,0)即为所求,则点P的横坐标为1.
16.已知P是直线3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A,B是切点.
(1)求四边形PACB面积的最小值;
(2)直线上是否存在点P,使∠BPA=60°,若存在,求出点P的坐标;若不存在,说明理由.
解:(1)如图,连接PC,由点P在直线3x+4y+8=0上,可设点P坐标为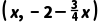 .
.
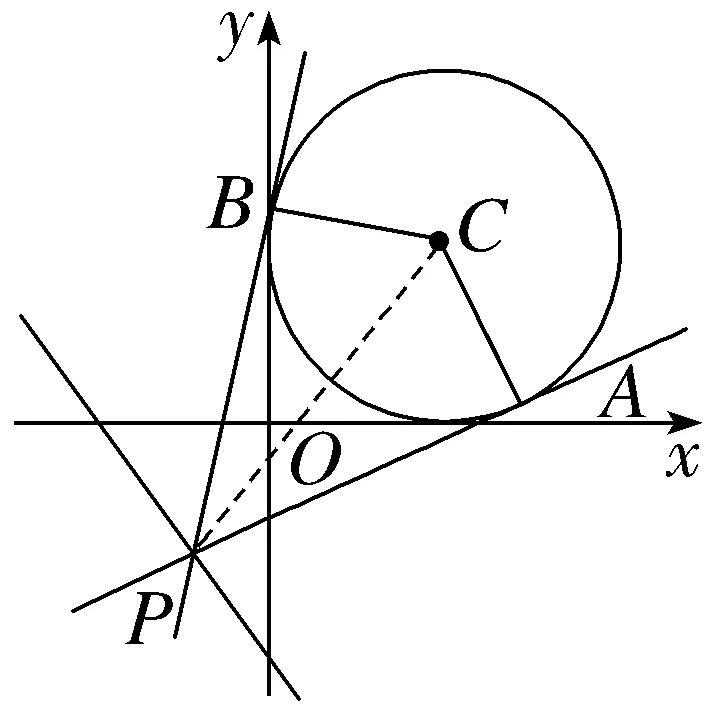
圆的方程可化为(x-1)2+(y-1)2=1,
所以S四边形PACB=2S△PAC=2×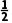 ×|AP|×|AC|=|AP|.
×|AP|×|AC|=|AP|.
因为|AP|2=|PC|2-|CA|2=|PC|2-1,
所以当|PC|最小时,|AP|最小.
因为|PC|2=(1-x)2+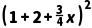 =(
=(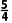 x+1)2+9.
x+1)2+9.
所以当x=-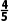 时,|PC
时,|PC =9.
=9.
所以|AP|min=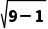 =2
=2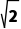 .
.
即四边形PACB面积的最小值为2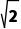 .
.
(2)由(1)知圆心C到点P距离为3是C到直线上点的最小值,若∠APB=60°,则需|PC|=2,这是不可能的,所以这样的点P不存在.

通过网盘分享的文件:25-26学年同步培优讲义
链接: https://pan.baidu.com/s/1y0bSGZE1YoJg8gMTXiqQoA?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享