与面EFCB所成的二面角为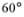 .
.
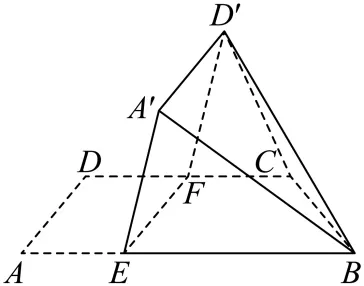
(1)证明: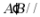 平面
平面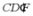 ;
;
(2)求面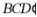 与面
与面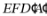 所成的二面角的正弦值.
所成的二面角的正弦值.
18.已知函数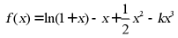 ,其中
,其中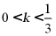 .
.
(1)证明: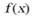 在区间
在区间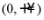 存在唯一的极值点和唯一的零点;
存在唯一的极值点和唯一的零点;
(2)设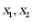 分别为
分别为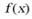 在区间
在区间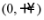 的极值点和零点.
的极值点和零点.
(i)设函数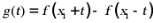 ·证明:
·证明: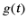 在区间
在区间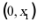 单调递减;
单调递减;
(ii)比较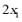 与
与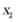 的大小,并证明你的结论.
的大小,并证明你的结论.
19.甲、乙两人进行乒乓球练习,每个球胜者得1分,负者得0分.设每个球甲胜的概率为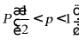 ,乙胜的概率为q,,且各球的胜负相互独立,对正整数
,乙胜的概率为q,,且各球的胜负相互独立,对正整数 ,记
,记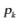 为打完k个球后甲比乙至少多得2分的概率,
为打完k个球后甲比乙至少多得2分的概率,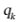 为打完k个球后乙比甲至少多得2分的概率.
为打完k个球后乙比甲至少多得2分的概率.
(1)求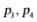 (用p表示).
(用p表示).
(2)若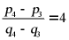 ,求p.
,求p.
(3)证明:对任意正整数m,.
1.C
【分析】由平均数的计算公式即可求解.
【详解】样本数据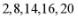 的平均数为
的平均数为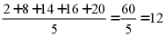 .
.
故选:C.
2.A
【分析】由复数除法即可求解.
【详解】因为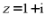 ,所以
,所以 .
.
故选:A.
3.D
【分析】求出集合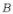 后结合交集的定义可求
后结合交集的定义可求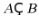 .
.
【详解】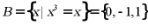 ,故
,故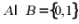 ,
,
故选:D.
4.C
【分析】移项后转化为求一元二次不等式的解即可.
【详解】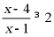 即为
即为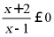 即
即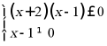 ,故
,故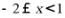 ,
,
故解集为 ,
,
故选:C.
5.A
【分析】由余弦定理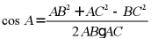 直接计算求解即可.
直接计算求解即可.
【详解】由题意得 ,
,
又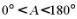 ,所以
,所以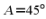 .
.
故选:A
6.C
【分析】先由直线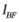 求出焦点
求出焦点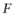 和
和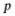 即抛物线
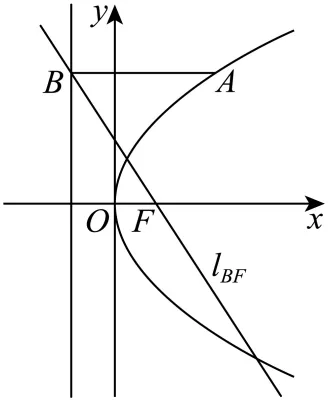
即抛物线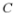 的方程,进而依次得抛物线的准线方程和点B,从而可依次求出
的方程,进而依次得抛物线的准线方程和点B,从而可依次求出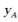 和
和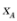 ,再由焦半径公式即可得解.
,再由焦半径公式即可得解.
【详解】对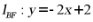 ,令
,令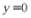 ,则
,则 ,
,
所以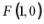 即抛物线
即抛物线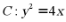 ,故抛物线的准线方程为
,故抛物线的准线方程为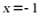 ,
,
故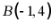 ,则
,则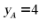 ,代入抛物线
,代入抛物线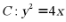 得
得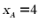 .
.
所以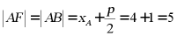 .
.
故选:C
7.B
【分析】由等差数列前n项和公式结合题意列出关


通过网盘分享的文件:【免费下载】高考真题【山西】2025年高考全国二卷数学高考真题解析word版含解析学生版教师版
链接: https://pan.baidu.com/s/1onwUKqePAXMkDRQiZ_qc3Q?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享