
(满分150分时间120分钟)
一、选择题:(每小题3分,共45分)
1. 如果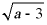 有意义,则a的取值范围是( )
有意义,则a的取值范围是( )
A. B. C. D.
【答案】C
【解析】
【分析】根据二次根式的被开方数是非负数,可得不等式,根据解不等式,可得答案.
【详解】解:由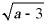 有意义得:
有意义得: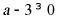
解得: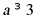 .
.
故选:C.
【点睛】本题主要考查了二次根式和分式有意义的条件,二次根式的被开方数是非负数.分式的分母不能等于0.
2. 下列二次根式中与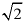 是同类二次根式的是()
是同类二次根式的是()
A. 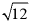 B.
B. 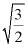 C.
C. 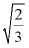 D.
D. 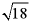
【答案】D
【解析】
【分析】同类二次根式的定义:化为最简二次根式后被开方数相同的二次根式.
【详解】解:A、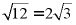 、
、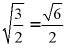 、
、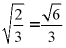 ,均不是同类二次根式,故错误;
,均不是同类二次根式,故错误;
D、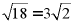 ,符合同类二次根式的定义,本选项正确;
,符合同类二次根式的定义,本选项正确;
故选D.
【点睛】本题主要考查最简二次根式,熟练掌握最简二次根式是解题的关键.
3. 下列计算准确的是()
A. 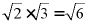 B.
B. 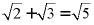 C.
C. 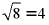 D.
D. 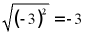
【答案】A
【解析】
【分析】根据二次根式的运算法则逐项判断即可.
【详解】解:A、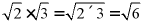 ,故正确;
,故正确;
B、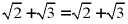 ,故错误;
,故错误;
C、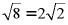 ,故错误;
,故错误;
D、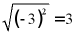 ,故错误;
,故错误;
故选:A.
【点睛】本题考查二次根式的运算,解题的关键是掌握二次根式相关的运算法则.
4. 若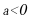 ,化简
,化简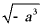 的结果是()
的结果是()
A. 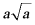 B.
B. 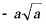 C.
C. 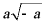 D.
D. 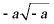
【答案】D
【解析】
【分析】根据二次根式的性质及幂的乘方运算的逆运算化简即可得到答案.
【详解】解: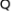
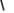
故选:D.
【点睛】本题考查二次根式化简,熟练掌握二次根式的性质及幂的乘方运算的逆运算化简是解决问题的关键.
5. 在式子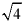 中,最简二次根式的个数是()
中,最简二次根式的个数是()
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
【分析】根据最简二次根式的定义:满足下列两个条件的二次根式,叫做最简二次根式:(1)被开方数的因数是整数,因式是整式; (2)被开方数中不含能开得尽方的因数或因式,逐一判断即可.
【详解】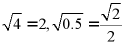 ,这两项均不是最简二次根式,则排除,
,这两项均不是最简二次根式,则排除,
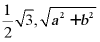 ,均符合二次根式的定义,
,均符合二次根式的定义,
故选:B.
【点睛】本题考查最简二次根式的定义,充分理解最简二次根式的定义是解题关键.
6. 已知: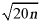 是整数,则满足条件的最小正整数
是整数,则满足条件的最小正整数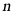 为()
为()
A. 2B. 3C. 4D. 5
【答案】D
【解析】
【详解】试题解析:∵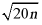 =
=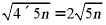 ,且
,且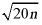 是整数,
是整数,
∴2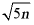 是整数,即5n是完全平方数,
是整数,即5n是完全平方数,
∴n 最小正整数为5.
最小正整数为5.
故选D.
点睛:主要考查了乘除法法则和二次根式有意义的条件.二次根式有意义的条件是被开方数是非负数.二次根式的运算法则:乘法法则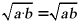 .除法法则
.除法法则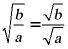 .解题关键是分解成一个完全平方数和一个代数式的积的形式.
.解题关键是分解成一个完全平方数和一个代数式的积的形式.
7. 用配方法解方程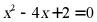 ,下列配方正确的是()
,下列配方正确的是()
A. 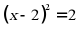 B.
B. 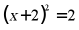 C.
C. 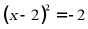 D.
D. 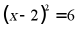
【答案】A
【解析】
【分析】根据配方法求解即可.
【详解】解: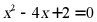
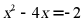
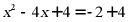
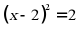 .
.
故选A.
【点睛】题目主要考查配方法解一元二次方程,熟练掌握配方法 解题关键.
解题关键.
8. 一元二次方程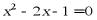 的根的情况为( )
的根的情况为( )
A. 有两个相等的实数根B. 有两个不相等的实数根C. 只有一个实数根D. 没有实数根
【答案】B
【解析】
【分析】根据一元二次方程根的判别式判断根的情况:当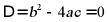 时,方程有两个相等实数根;当
时,方程有两个相等实数根;当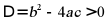 时,方程有两个不相等实数根;当
时,方程有两个不相等实数根;当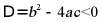 时,方程无实数根;该一元二次方程
时,方程无实数根;该一元二次方程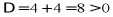 ,即有两个不相等实数根,可得答案B.
,即有两个不相等实数根,可得答案B.
【详解】解: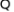 一元二次方程
一元二次方程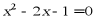
∴判别式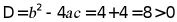 ,
,
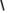 方程有两个不相等的实数根.
方程有两个不相等的实数根.
故选B



通过网盘分享的文件:【免费下载】精编江苏省苏州市吴中区卧佛镇中学20232024学年九年级上学期第一学月月考数学试题
链接: https://pan.baidu.com/s/1Fmbs3v0A69QOxXFgaBkJrA?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享