 2022~2023学年第一学期
2022~2023学年第一学期
九年级第一次阶段知识摸底数学试卷
一、选择题(每小题3分,共36分)
1. 已知关于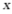 的一元二次方程
的一元二次方程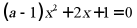 ,则常数
,则常数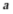 满足的条件是()
满足的条件是()
A. B. C. D. 无法确定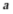 的值
的值
2. 下列关系式中,是二次函数关系的是()
A. 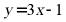 B.
B. 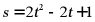 C.
C. 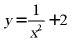 D.
D. 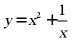
3. 如果2是方程x²−3x+k=0 一个根,则此方程的另一根为()
一个根,则此方程的另一根为()
A. 2B. 1C. −1D. −2
4. 一元二次方程x2-8x=48可表示成(x-a)2=48+b的形式,其中a,b为整数,求a+b之值为何( )
A. 20B. 12C. -12D. -20
5. 下列一元二次方程中,没有实数根 是()
是()
A. 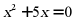 B.
B. 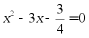
C. 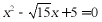 D.
D. 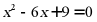
6. 一次排球赛,计划安排7天,每天安排4场,赛制是参赛的每个队之间都要比赛一场.设有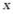 个球队参加比赛,则
个球队参加比赛,则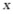 满足的方程是()
满足的方程是()
A. 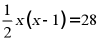 B.
B. 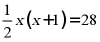
C. 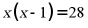 D.
D. 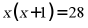
7. 如图,在宽为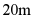 ,长为
,长为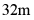 的矩形的广场上,有两条同宽且互相垂直的小路,余下部分绿地.若绿地面积为
的矩形的广场上,有两条同宽且互相垂直的小路,余下部分绿地.若绿地面积为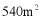 ,小路宽为
,小路宽为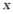 ,则
,则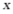 满足的方程是()
满足的方程是()

A. 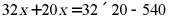 B.
B. 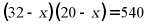
C. 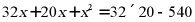 D.
D. 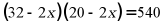
8. 某区今年教育经费投入2500万元,计划用两年时间再投入6600万元,使全区达到现代化办学标准,设每年教育经费投入的年平均增长率为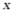 ,则
,则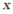 满足的方程是()
满足的方程是()
A. 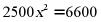 B.
B. 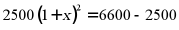
C. 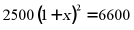 D.
D. 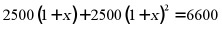
9. 二次函数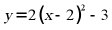 的顶点坐标是()
的顶点坐标是()
A. 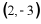 B.
B. 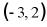 C.
C. 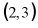 D.
D. 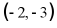
10. 将抛物线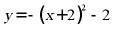 向上平移1个单位长度,则平移后抛物线的解析式是()
向上平移1个单位长度,则平移后抛物线的解析式是()
A
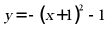 B.
B. 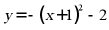 C.
C. 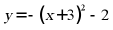 D.
D. 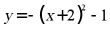
11. 已知抛物线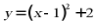 ,下列结论不正确的是()
,下列结论不正确的是()
A. 顶点在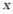 轴上方B. 对称轴在
轴上方B. 对称轴在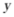 轴右侧C. 顶点是抛物线的最低点D. 与
轴右侧C. 顶点是抛物线的最低点D. 与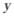 轴的交点是
轴的交点是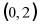
12. 下列各点,在抛物线设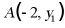 是抛物线
是抛物线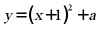 上的三点,则
上的三点,则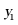 的大小关系为()
的大小关系为()
A. 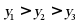 B.
B. 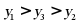 C.
C. 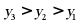 D.
D. 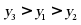
二、填空题(每小题3分,共18分)
13. 一元二次方程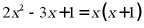 化为一般形式是__________.
化为一般形式是__________.
14. 若抛物线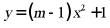 的开口向下,则常数
的开口向下,则常数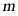 的取值范围是__________.
的取值范围是__________.
15. 如关于x的一元二次方程(m﹣1)x2+5x+m2﹣1=0一个根为0,则m=_____.
16. 关于x 的一元二次方程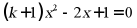 有两个实数根,则k的取值范围是_________
有两个实数根,则k的取值范围是_________
17. 若m是方程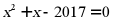 的一个实数根,则多项式
的一个实数根,则多项式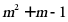 的值是__________.
的值是__________.
18. 若关于x的一元二次方程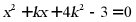 的两个实数根分别是
的两个实数根分别是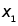 ,且满足
,且满足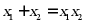 __________.
__________.
三、解答题
19. 解下列方程
(1)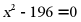 ;
;
(2)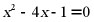 .
.
20. 解下列方程
(1)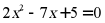 ;
;
(2)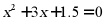 .
.
21. 解下列方程
(1)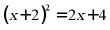 ;
;
(2)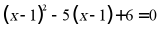 .
.
22. 已知二次函数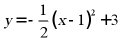 .
.
(1)选取适当的数值填入下表,并画出该抛物线.
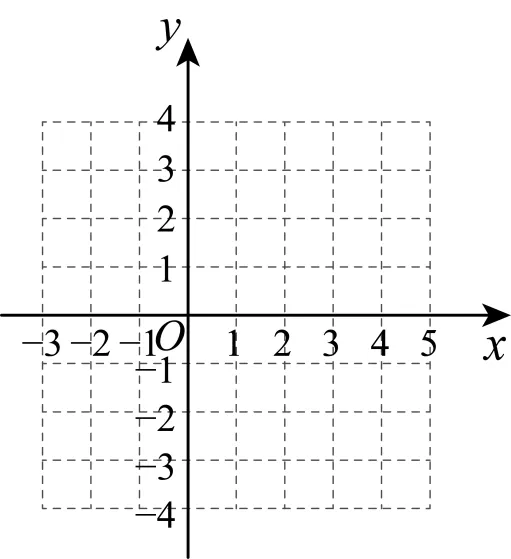
(2)若点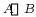 分别为抛物线与
分别为抛物线与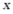 轴的交点(点
轴的交点(点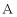 在点
在点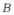 左边),则点
左边),则点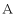 (__________),
(__________),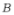 (__________).
(__________).
(3)当自变量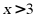 时,函数值
时,函数值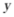 的取值范围是__________.
的取值范围是__________.
23. 如图,学校为美化环境,在靠墙的一侧设计了一块矩形花圃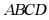 ,其中,墙长
,其中,墙长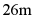 ,花圃三边外围用管笆围起,共用篱笆
,花圃三边外围用管笆围起,共用篱笆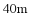 .
.
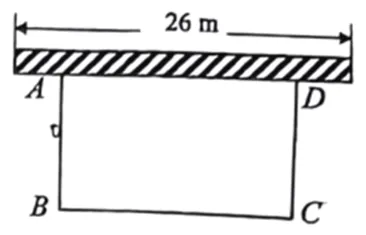
(1)若花圃的面积为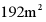 ,求花圃一边
,求花圃一边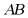 的长;
的长;
(2)花圃的面积能达到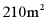 吗?说明理由.
吗?说明理由.
24. 已知某商品 进价每件是40元,现在的售价每件是60元,每周可卖出300件.市场调查反映,若调整价格,每涨价1元,每周可少卖出10件.设该商品每件涨价
进价每件是40元,现在的售价每件是60元,每周可卖出300件.市场调查反映,若调整价格,每涨价1元,每周可少卖出10件.设该商品每件涨价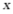 元
元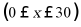 .
.
(1)根据题意填写下表:
| 售价(元/件) | 每件利润(元) | 每周销量(件) | 每周利润(元) |
现在 | 60 | 20 | 300 | 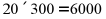
|
涨价后 | | | | |
(2)若计划每周的利润为6160元,该商品每件应涨价多少?
25. 已知抛物线y=a(x﹣1)2﹣3(a≠0) 图象与y轴交于点A(0,﹣2),顶点为B.
图象与y轴交于点A(0,﹣2),顶点为B.
(1)试确定a的值,并写出B点的坐标;
(2)若一次函数的图象经过A、B两点,试写出一次函数的解析式;
(3)试在x轴上求一点P,使得△PAB的周长取最


通过网盘分享的文件:【免费下载】精编天津市北辰区实验中学20232024学年九年级上学期月考数学试题
链接: https://pan.baidu.com/s/1CLhvxBp6xmTrGqFxptAzEQ?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享