【免费下载】25-26学年同步培优讲义第2课时 函数奇偶性的应用(教师版

第2课时函数奇偶性的应用

角度1定义法求函数解析式

【例1】函数f（x）是定义域为R的奇函数，当x＞0时，f（x）＝－x＋1，求f（x）的解析式.

解：设x＜0，则－x＞0，

∴f（－x）＝－（－x）＋1＝x＋1，

又∵函数f（x）是定义域为R的奇函数，

∴f（－x）＝－f（x）＝x＋1，

∴当x＜0时，f（x）＝－x－1.

又x＝0时，f（0）＝0，

∴f（x）＝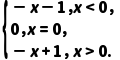

通性通法

如果已知函数的奇偶性和一个区间[a，b]上的解析式，求关于原点的对称区间[－b，－a]上的解析式，其解决思路为：

（1）“求谁设谁”，即在哪个区间上求解析式，x就应在哪个区间上设；

（2）利用已知区间上的解析式进行代入；

（3）利用f（x）的奇偶性写出－f（x）或f（－x），从而解出f（x）.

提醒若函数f（x）的定义域内含0且为奇函数，则必有f（0）＝0，但若为偶函数，未必有f（0）＝0.

角度2　方程组法求函数解析式

【例2】设f（x）是偶函数，g（x）是奇函数，且f（x）＋g（x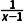）＝f（x），g（x）的解析式.

解：∵f（x）是偶函数，g（x）是奇函数，∴f（－x）＝f（x），g（－x）＝－g（x），

由f（x）＋g（x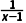）＝①

用－x代替x，

得f（－x）＋g（－x）＝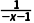

∴f（x）－g（x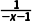）＝②

（①＋②）÷2，得f（x）＝；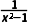

（①－②）÷2，得g（x）＝.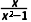

通性通法

已知函数f（x），g（x）的组合运算与奇偶性，把x换为－x，构造方程组求解.

【跟踪训练】

1.已知函数f（x）为R上的偶函数，且当x＜0时，f（x）＝x（x－1），则当x＞0时，f（x）＝x（x＋1）.

解析：当x＞0时，－x＜0，则f（－x）＝－x（－x－1）＝x（x＋1），因为函数f（x）为R上的偶函数，故当x＞0时，f（x）＝f（－x）＝x（x＋1）.

2.已知函数f（x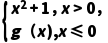）＝为奇函数，则g（x）＝.

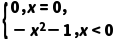解析：因为函数f（x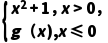）＝为奇函数，所以f（0）＝g（0）＝0.设x＜0，则－x＞0，f（－x）＝（－x）²＋1＝x²＋1，所以f（x）＝g（x）＝－f（－x）＝－x²－1.综上可得g（x）＝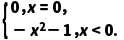

【例3】若对于任意实数x总有f（－x）＝f（x），且f（x）在区间（－∞，－1]上单调递增，则（）

A.f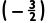＜f（－1）＜f（2）

B.f（2）＜f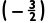＜f（－1）

C.f（2）＜f（－1）＜f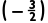

D.f（－1）＜f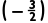＜f（2）

解析：B由题意得，f（x）为偶函数，∴f（2）＝f（－2）.又f（x）在区间（－∞，－1]上单调递增，且－2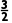＜－＜－1，∴f（2）＝f（－2）＜f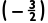＜f（－1），故选B.

通性通法

利用函数的奇偶性与单调性比较大小的方法

（1）自变量在同一单调区间上，直接利用函数的单调性比较大小；

（2）自变量不在同一单调区间上，需利用函数的奇偶性把自变量转化到同一单调区间上，然后利用单调性比较大小.

【跟踪训练】

1.已知f（x）是奇函数，且在区间[0，＋∞）上单调递增，则f（－0.5），f（－1），f（0）的大小关系是（）

A.f（－0.5）＜f（0）＜f（－1）

B.f（－1）＜f（－0.5）＜f（0）

C.f（0）＜f（－0.5）＜f（－1）

D.f（－1）＜f（0）＜f（－0.5）

解析：B∵函数f（x）为奇函数，且f（x）在区间[0，＋∞）上单调递增，∴f（x）在R上是增函数，∴f（－1）＜f（－0.5）＜f（0）.

2.已知函数f（x）在[－5，5]上是偶函数，在[0，5]上是单调函数，且f（－4）＜f（－2），则下列不等式一定成立的是（）

A.f（－1）＜f（3）B.f（2）＜f（3）

C.f（－3）＜f（5）D.f（0）＞f（1）

解析：D因为函数f（x）在[－5，5]上是偶函数，且f（－4）＜f（－2），所以f（4）＜f（2）.又f（x）在[0，5]上是单调函数.所以f（x）在[0，5]上单调递减，从而f（0）＞f（1），故选D.

【例4】已知定义在[－2，2]上的奇函数f（x）在区间[0，2]上单调递减，若f（1－m）＜f（m），求实数m的取值范围.

解：因为f（x）在区间[－2，2]上为奇函数，且在区间[0，2]上单调递减，所以f（x）在区间[－2，2]上是减函数.

又f（1－m）＜f（m），所以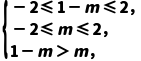

即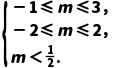解得－1≤m＜.

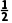故实数m的取值范围是.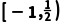

【母题探究】

（变条件）若将本例中的“奇函数”改为“偶函数”，把区间“[0，2]”改为“[－2，0]”，其他条件不变，求实数m的取值范围.

解：因为函数为[－2，2]上的偶函数，又函数在区间[－2，0]上单调递减，所以函数在区间[0，2]上单调递增，

原不等式可化为f（｜1－m｜）＜f（｜m｜），

故可得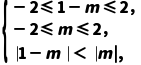即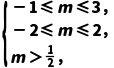

解得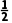＜m≤2.故实数m的取值范围为.

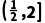通性通法

利用函数奇偶性与单调性解不等式的步骤

（1）将所给的不等式转化为两个函数值的大小关系；

（2）由已知或利用奇偶性得出区间上的单调性，再利用单调性“脱去”函数的对应法则“f”，转化为解不等式（组）的问题.

提醒在转化时，自变量的取值必须在同一单调区间上；当不等式一边没有写成“f（x）”的形式时，需转化为“f（x）”的形式，如0＝f（1），f（x－1）＜0，则f（x－1）＜f（1）.注意偶函数f（x）中结论f（x）＝f（｜x｜）的灵活运用.

【跟踪训练】

已知函数f（x）是定义在（－2，2）上的奇函数，又是增函数.解关于t的不等式f（t－1）＋f（2t－3）＜0.

解：因为f（x）为（－2，2）上的奇函数，所以f（t－1）＋f（2t－3）＜0可化为f（t－1）＜f（3－2t），

又因为函数f（x）在（－2，2）上是增函数，所以－2＜t－1＜3－2t＜2，解得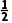＜t＜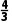

所以关于t的不等式f（t－1）＋f（2t－3）＜0的解集为.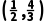

1.已知函数f（x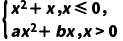）＝为奇函数，则a＋b＝（）

A.－1B.1C.0D.2

解析：C当x＜0时，－x＞0，∵f（x）为奇函数，∴f（－x）＝－f（x）.即ax²－bx＝－x²－x，∴a＝－1，b＝1.故a＋b＝0.

2.已知函数y＝f（x）是定义在R上的偶函数，且在[2，6]上单调递减，则f（－5）与f（3）的大小关系是f（－5）＜f（3）.

解析：因为f（x）是偶函数，所以f（－5）＝f（5），因为f（x）在[2，6]上单调递减，所以f（5）＜f（3），即f（－5）＜f（3）.

3.已知定义在R上的偶函数f（x）在（－∞，0]上单调递增，若f（a）＞f（3），则实数a的取值范围是（－3，3）.

解析：由题意可知｜a｜＜3，解得－3＜a＜3.

4.已知f（x）是定义在R上的奇函数，且当x≥0时，f（x）＝2x－x².求当x＜0时，f（x）的解析式.

解：当x＜0时，－x＞0，

于是f（－x）＝2（－x）－（－x）²＝－2x－x².

因为f（x）是定义在R上的奇函数，

所以f（x）＝－f（－x）＝－（－2x－x²）＝2x＋x^2，

即f（x）＝2x＋x²（x＜0）.

1.下列函数中，既是奇函数又是增函数的为（）

A.y＝x²B.y＝x⁵＋1

C.y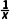＝D.y＝x³

解析：DA选项，y＝x²是偶函数，故A错误；B选项，y＝x⁵＋1是非奇非偶函数，故B错误；C选项，y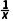＝在（－∞，0），（0，＋∞）上单调递减，故C错误；D选项，y＝x³既是奇函数又是增函数，故D正确.故选D.

2.已知偶函数f（x）的定义域为R，当x∈[0，＋∞）时，f（x）单调递增，则f（－2），f（π），f（－3）的大小关系是（）

A.f（π）＞f（－2）＞f（－3）

B.f（π）＞f（－3）＞f（－2）

C.f（π）＜f（－2）＜f（－3）

D.f（π）＜f（－3）＜f（－2）

解析：B因为f（x）为偶函数，所以f（－2）＝f（2），f（－3）＝f（3）.又当x∈[0，＋∞）时，f（x）单调递增，且π＞3＞2，所以f（π）＞f（3）＞f（2），即f（π）＞f（－3）＞f（－2）.故选B.

3.若奇函数f（x）在区间[3，6]上单调递增，且在区间[3，6]上的最大值为7，最小值为－1，则f（－3）＋2f（－6）＝（）

A.13B.－13C.5D.－5

解析：B由f（x）在区间[3，6]上单调递增，在区间[3，6]上的最大值为7，最小值为－1，得f（3）＝－1，f（6）＝7.∵f（x）是奇函数，∴f（－3）＝－f（3）＝1，f（－6）＝－f（6）＝－7，∴f（－3）＋2f（－6）＝1＋2×（－7）＝－13.

4.已知函数f（x）是奇函数，函数g（x）＝f（x）－2，则g（20）＋g（－20）＝（）

A.2B.0

C.－2D.－4

解析：D根据题意，函数f（x）是奇函数，则f（x）＋f（－x）＝0，则g（x）＋g（－x）＝f（x）－2＋f（－x）－2＝0－4＝－4，则g（20）＋g（－20）＝－4，故选D.

5.（多选）已知定义在区间[－7，7]上的一个偶函数，它在[0，7]上的图象如图，则下列说法正确的有（）

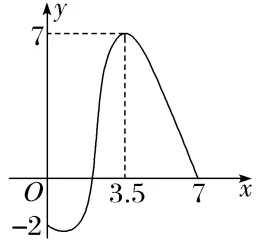
A.这个函数有两个单调递增区间

B.这个函数有三个单调递减区间

C.这个函数在其定义域内有最大值7

D.这个函数在其定义域内有最小值－7

解析：BC根据偶函数在[0，7]上的图象及其对称性，作出其在[－7，7]上的图象，如图所示.由图象可知这个函数有三个单调递增区间，有三个单调递减区间，在其定义域内有最大值7，最小值不是－7，故选B、C.

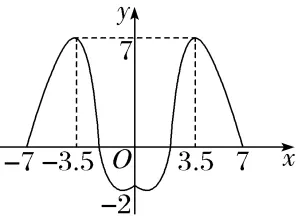
6.（多选）已知函数f（x）是R上的奇函数，且当x≥0时，f（x）＝x²＋x＋a－2，则（）

A.a＝2B.f（2）＝2

C.f（x）是R上的增函数D.f（－3）＝－12

解析：ACD　f（x）是R上的奇函数，故f（0）＝a－2＝0，得a＝2，故A正确.f（2）＝4＋2＝6，故B错误.当x≥0时，f（x）＝x²＋x在[0，＋∞）上单调递增，利用奇函数的对称性可知，f（x）在（－∞，0]上单调递增，故f（x）是R上的增函数，故C正确.f（－3）＝－f（3）＝－9－3＝－12，故D正确.故选A、C、D.

7.已知f（x）为奇函数，g（x）＝f（x）＋9，g（－2）＝3，则f（2）＝　6　.

解析：∵f（x）为奇函数，∴f（－x）＝－f（x）.∵g（x）＝f（x）＋9，∴g（－x）＝f（－x）＋9＝－f（x）＋9，∴f（x）＝9－g（－x）.∵g（－2）＝3，∴f（2）＝9－g（－2）＝9－3＝6.

8.若f（x）＝（m－1）x²＋6mx＋2是偶函数，则f（0），f（1），f（－2）从小到大的排列是f（－2）＜f（1）＜f（0）.

解析：∵f（x）是偶函数，∴f（－x）＝f（x）恒成立，即（m－1）x²－6mx＋2＝（m－1）x²＋6mx＋2恒成立，∴m＝0，即f（x）＝－x²＋2.∵f（x）的图象开口向下，对称轴为y轴，在[0，＋∞）上单调递减，∴f（2）＜f（1）＜f（0），又∵f（x）＝－x²＋2为偶函数，∴f（2）＝f（－2）.即f（－2）＜f（1）＜f（0）.

9.已知f（x）是定义在R上的偶函数，且在区间（－∞，0）上单调递增.若f（－3）＝0，则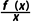＜0的解集为{x｜－3＜x＜0或x＞3}.

解析：∵f（x）是定义在R上的偶函数，且在区间（－∞，0）上单调递增，∴f（x）在区间（0，＋∞）上单调递减.∴f（3）＝f（－3）＝0.当x＞0时，由f（x）＜0，解得x＞3；当x＜0时，由f（x）＞0，解得－3＜x＜0.故所求解集为{x｜－3＜x＜0或x＞3}.

10.已知f（x）是定义在（－1，1）上的奇函数，且f（x）在（－1，1）上是减函数，解不等式f（1－x）＋f（1－2x）＜0.

解：∵f（x）是定义在（－1，1）上的奇函数，

由f（1－x）＋f（1－2x）＜0，得

f（1－x）＜－f（1－2x），即f（1－x）＜f（2x－1）.

又∵f（x）在（－1，1）上是减函数，

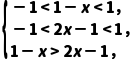∴解得0＜x＜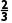

∴原不等式的解集为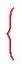x＜x＜.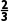

11.已知偶函数f（x）在[0，＋∞）上单调递增，且f（－2）＝3，则满足f（2x－3）＜3的x的取值范围是（）

A.∪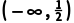

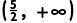
B.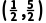

C.∪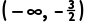

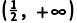
D.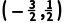

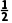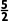解析：B因为偶函数f（x）在[0，＋∞）上单调递增，且f（－2）＝3，所以f（x）在（－∞，0）上单调递减，且f（2）＝3.因为f（2x－3）＜3，所以－2＜2x－3＜2，所以＜x＜.故选B.

12.若函数y＝f（x）是奇函数，且函数F（x）＝af（x）＋bx＋2在（0，＋∞）上有最大值8，则函数y＝F（x）在（－∞，0）上有（）

A.最大值－8B.最小值－8

C.最小值－6D.最小值－4

解析：D∵y＝f（x）和y＝x都是奇函数，∴T（x）＝af（x）＋bx也为奇函数.又∵F（x）＝af（x）＋bx＋2在（0，＋∞）上有最大值8，∴T（x）＝af（x）＋bx在（0，＋∞）上有最大值6，∴T（x）＝af（x）＋bx在（－∞，0）上有最小值－6，∴F（x）＝af（x）＋bx＋2在（－∞，0）上有最小值－4.

13.若函数f（x）＝（x＋a）（bx＋2a）（常数a，b∈R）是偶函数，且它的值域为（－∞，4]，则该函数的解析式f（x）＝－2x²＋4　.

解析：∵f（x）＝（x＋a）（bx＋2a）＝bx²＋（2a＋ab）x＋2a²是偶函数，∴图象关于y轴对称，∴2a＋ab＝0，∴a＝0或b＝－2.若a＝0，则函数为f（x）＝bx^2，当b为正数时，值域为[0，＋∞），不符合题意；当b为负数时，值域为（－∞，0]，不符合题意；当b＝0时，值域为{0}，不符合题意.若b＝－2，则函数为f（x）＝－2x²＋2a².又∵值域为（－∞，4]，∴2a²＝4，∴f（x）＝－2x²＋4.

14.已知f（x）是定义在R上的函数，设g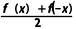（x）＝（x）＝.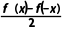

（1）试判断 g（x）与h（x）的奇偶性；

（2）试判断g（x），h（x）与f（x）的关系；

（3）由此你能猜想出什么样的结论？

解：（1）∵g（－x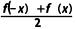）＝＝g（x），h（－x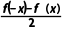）＝＝－h（x），∴g（x）是偶函数，h（x）是奇函数.

（2）g（x）＋h（x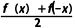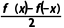）＝＋＝f（x）.

（3）如果一个函数的定义域关于原点对称，那么这个函数就一定可以表示为一个奇函数与一个偶函数的和.

15.（多选）关于定义在R上的偶函数f（x），当x≥0时，f（x）＝x²＋2x，则下列说法正确的是（）

A.当x＜0时，f（x）＝x²－2x

B.函数f（x）在定义域R上为增函数

C.不等式f（3x－2）＜8的解集为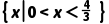

D.不等式f（x）－x²－x－1＜0恒成立

解析：AC对于A，设x＜0，则－x＞0，所以f（－x）＝x²－2x，又f（x）是偶函数，所以f（x）＝f（－x）＝x²－2x，即当x＜0时，f（x）＝x²－2x，故A中说法正确；对于B，当x≥0时，f（x）＝x²＋2x函数f（x）的图象的对称轴为直线x＝－1.所以当x≥0时，f（x）单调递增，由偶函数的图象关于y轴对称得，f（x）在（－∞，0）上为减函数，故B中说法错误；对于C，当x∈[0，＋∞）时，令f（x）＝x²＋2x＝8，解得x₁＝2，x₂＝－4（舍去），即f（2）＝8，所以不等式f（3x－2）＜8即f（3x－2）＜f（2），又f（x）在R上为偶函数，则｜3x－2｜＜2⇒0＜x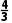＜C中说法正确；对于D，当x＜0时，f（x）＝x²－2x，f（x）－x²－x－1＝x²－2x－x²－x－1＝－3x－1不恒小于0.当x≥0时，f（x）＝x²＋2x，f（x）－x²－x－1＝x²＋2x－x²－x－1＝x－1不恒小于0，故D中说法错误.故选A、C.

16.设f（x）是定义在R上的奇函数，且对任意a，b∈R，当a＋b≠0时，都有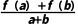＞0.

（1）若a＞b，试比较f（a）与f（b）的大小关系；

（2）若f（1＋m）＋f（3－2m）≥0，求实数m的取值范围.

解：（1）因为a＞b，所以a－b＞0，

由题意得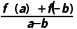＞0，

所以f（a）＋f（－b）＞0.

又f（x）是定义在R上的奇函数，

所以f（－b）＝－f（b），

所以f（a）－f（b）＞0，即f（a）＞f（b）.

（2）由（1）知f（x）为R上的增函数，

因为f（1＋m）＋f（3－2m）≥0，

所以f（1＋m）≥－f（3－2m），

即f（1＋m）≥f（2m－3），

所以1＋m≥2m－3，所以m≤4.

所以实数m的取值范围为（－∞，4].

通过网盘分享的文件：25-26学年同步培优讲义

链接: https://pan.baidu.com/s/1y0bSGZE1YoJg8gMTXiqQoA?pwd=4321 提取码: 4321 

--来自百度网盘超级会员v8的分享