 学年三门初级中学九年级(上)月考数学试卷
学年三门初级中学九年级(上)月考数学试卷
一.选择题
二.(共10小题,每小题4分)
1. 下列图形中,是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
2. 圆锥底面圆 半径为2,母线长为4,则该圆锥的侧面积为( )
半径为2,母线长为4,则该圆锥的侧面积为( )
A. 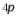 B.
B. 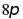 C.
C. 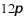 D. 4
D. 4
3. 已知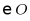 直径为6,线段
直径为6,线段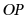 的长度为2,则点P与
的长度为2,则点P与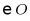 的位置关系是( )
的位置关系是( )
A. 点P在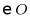 内B. 点P在
内B. 点P在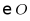 上C. 点P在
上C. 点P在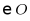 外D. 无法确定
外D. 无法确定
4. 某微信群规定,群内的每个人都要发一个红包,并保证群内其他人都能抢到且自己不能抢自己发的红包,若此次抢红包活动,群内所有人共收到1640个红包,设群内共有x个人,根据题意可列方程( )
A. 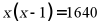 B.
B. 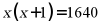
C. 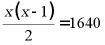 D.
D. 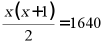
5. 下列说法中,正确的是( )
A. 平分弦的直径必垂直弦且平分弦所对的弧
B. 三点确定一个圆
C. 垂直于半径的直线是圆的切线
D. 同弧所对的圆周角相等
6. 如图,在矩形ABCD中,AB=1,BC=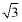 .将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
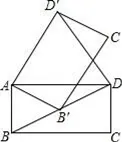
A. 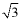 B.
B. 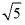 C.
C. 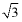 +1D. 2
+1D. 2
7. 如图,在边长为6的正方形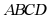 中,以
中,以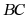 为直径画半圆,则阴影部分的面积是()
为直径画半圆,则阴影部分的面积是()
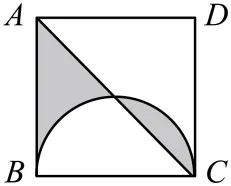
A. 9B. 6C. 3D. 12
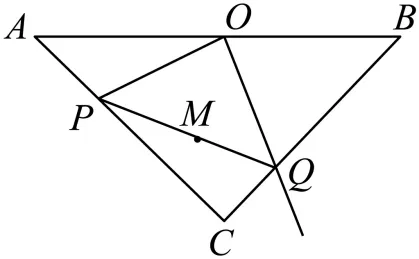
8. 若方程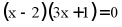 ,则
,则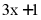 的值为
的值为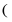
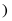
A
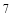 B.
B. 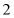 C.
C. 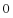 D. 7或
D. 7或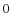
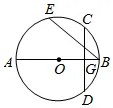
9. 如图,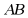 为
为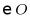 的直径,点C是弧
的直径,点C是弧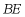 的中点.过点C作
的中点.过点C作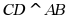 于点G,交
于点G,交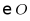 于点D,若
于点D,若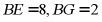 ,则
,则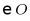 的半径长是()
的半径长是()
A. 5B. 6.5C. 7.5D. 8
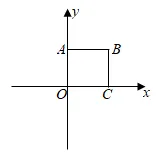
10. 定义:我们将顶点 横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形
横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形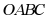 中,点
中,点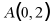 ,点
,点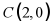 ,则互异二次函数
,则互异二次函数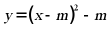 与正方形
与正方形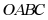 有交点时
有交点时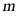 的最大值和最小值分别是()
的最大值和最小值分别是()
A. 4,-1B. 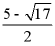 C. 4,0D.
C. 4,0D. 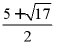
二.填空题(共6小题,每小题5分)
11. 将抛物线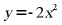 先向右平移2个单位,再向下平移3个单位得到新的抛物线______________.
先向右平移2个单位,再向下平移3个单位得到新的抛物线______________.
12. 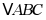 的三边分别为6,8,10,则
的三边分别为6,8,10,则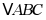 内切圆的半径为_____.
内切圆的半径为_____.
13. 随着新冠疫情趋于缓和,口罩市场趋于饱和,某N95口罩每盒原价为200元,连续两次降价后每盒的售价为72元,则平均每次下降的百分率为___________.
14. 定义新运算: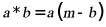 .若方程
.若方程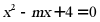 有两个相等正实数根,且
有两个相等正实数根,且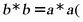 其中
其中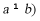 ,则
,则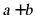 的值为_________.
的值为_________.
15. 如图,点E在正方形ABCD的边CB上,将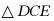 绕点D顺时针旋转90˚到
绕点D顺时针旋转90˚到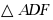 的位置,连接EF,过点D作EF的垂线,垂足为点H,于AB交于点G,若AG=4,BG=3,则BE的长为___________.
的位置,连接EF,过点D作EF的垂线,垂足为点H,于AB交于点G,若AG=4,BG=3,则BE的长为___________.
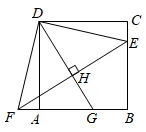
16. 如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为___________
三.解答题(共13小题)
17. 解方程:
(1)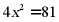 ;
;
(2)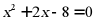 .
.
18. 已知关于x的一元二次方程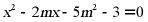 .
.
(1)当m=1时,试求出该方程的解;
(2)求证:不论m取任何值,该方程总有两个不相等的实数根.
19. 如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2).
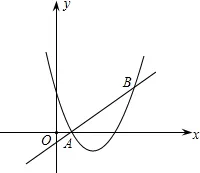
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
20. 如图所示,把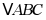 置于平面直角坐标系中,请你按下列要求分别画图:
置于平面直角坐标系中,请你按下列要求分别画图:
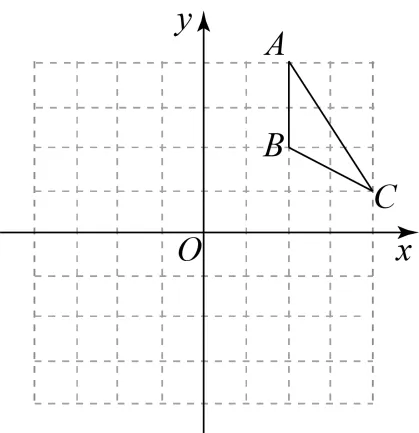
(1)画出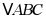 绕着原点O逆时针旋转
绕着原点O逆时针旋转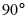 得到的
得到的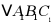 ;
;
(2)在(1)的基础上求点C经过的路径长.
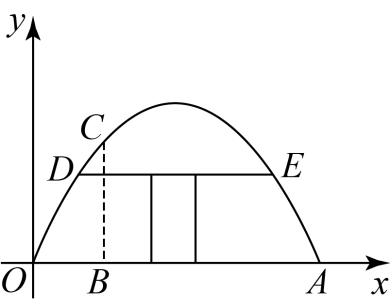
21. 有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示,已知OA=8米,距离O点2米处的棚高BC为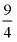 米.
米.
(1)求该抛物线的解析式;
(2)若借助横梁DE(DE∥OA)建一个门,要求门的高度为1.5米,求横梁DE的长度是多少米?
22. 如图,点A、B、C分别是⊙O上的点,∠B=60°,CD是⊙O的直径,CD=4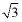 是CD延长线上的一点,且AP=AC.
是CD延长线上的一点,且AP=AC.
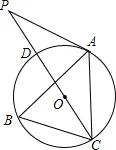
(1)求证:AP是⊙O的切线;
(2)求PD 长.
长.
23. 旋转与等腰直角三角形、正方形:把共顶点的一个等腰直角三角形和正方形中的一个绕一点旋转到一定位置,探究图形的几何性质,为我们提供一个动态的数学环境.
已知等腰直角三角形ABC和正方形BDEF有一个公共的顶点B,AB>BD.



通过网盘分享的文件:【免费下载】精编浙江省台州市三门初级中学20222023学年九年级上学期第三次月考数学试卷
链接: https://pan.baidu.com/s/15ZSUgVV-W5WQ8j5_U8SWEA?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享