



【例1】 定义在R上的偶函数y=f(x),其图象关于点(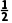 ,0)对称,且x∈[0,1]时,f(x)=-x+
,0)对称,且x∈[0,1]时,f(x)=-x+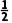 ,则f(
,则f(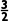 )=( )
)=( )
A.-1 B.0 C.1 D.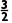
通性通法
1.函数图象关于直线对称
y=f(x)在定义域内恒满足的条件 | y=f(x)的图象的对称轴 |
f(a+x)=f(a-x) | 直线x=a |
f(x)=f(a-x) | 直线x=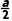 |
f(a+x)=f(b-x) | 直线x=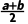 |
2.函数图象关于点对称
y=f(x)在定义域内恒满足的条件 | y=f(x)的图象的对称中心 |
f(a-x)=-f(a+x) | (a,0) |
f(x)=-f(a-x) | (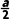 ,0) ,0) |
f(a+x)=-f(b-x) | (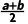 ,0) ,0) |
f(a+x)+f(b-x)=c | (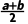 ) ) |
【跟踪训练】
1.已知函数f(x)的定义域为R,若f(1-x)为奇函数,f(x-1)为偶函数.设f(-2)=1,则f(2)=( )
A.-1B.0
C.1D.2
2.已知图象开口向上的二次函数f(x),对任意x∈R,都满足f(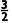 -x)=f(x+
-x)=f(x+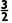 ),若f(x)在区间(a,2a-1)上单调递减,则实数a的取值范围为( )
),若f(x)在区间(a,2a-1)上单调递减,则实数a的取值范围为( )
A.(-∞,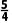 ]B.(1,
]B.(1,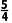 ]
]
C.[-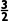 ,+∞)D.(-∞,2]
,+∞)D.(-∞,2]
【例2】 已知函数f(x)=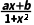 是定义在(-1,1)上的奇函数,且f(
是定义在(-1,1)上的奇函数,且f(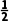 )=
)=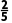 .
.
(1)确定函数f(x)的解析式;
(2)用定义法证明f(x)在(-1,1)上是增函数;
(3)解不等式:f(t-1)+f(t)<0.
通性通法
解决对称性、单调性和奇偶性综合问题的方法
(1)图象法:根据题意,作出符合要求的草图,便可得出结论;
(2)性质法:根据对称性、单调性和奇偶性的性质,逐步推导解决求值和比较大小的问题.
提醒使用性质要规范,切不可自创性质.
【跟踪训练】
已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)为奇函数,并且在定义域上是减函数,求不等式g(x)≤0的解集.
提示:完成课后作业 第三章 培优课