

培优课数列前n项和的求法
1.数列an=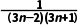 的前10项和S10=()
的前10项和S10=()
A.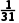 B.
B.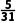 C.
C.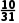 D.
D.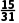
2.数列an=4n-1+n的前n项和Sn=()
A.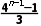 +
+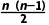 B.
B.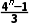 +
+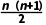 C.
C.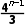 +
+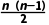 D.
D.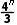 +
+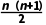
3.数列{an}的通项公式为an=(-1)n-1·(4n-3),则它的前100项之和S100=()
A.200B.-200C.400D.-400
4.德国数学家高斯是近代数学奠基者之一,在历史上有很大的影响.他幼年时就表现出超人的数学天赋,10岁时,他在进行1+2+3+…+100的求和运算时,就提出了倒序相加法的原理,该原理基于所给数据前后对应项的和呈现一定的规律生成,因此,此方法也称为高斯算法.已知数列an=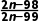 a1+a2+…+a98=()
a1+a2+…+a98=()
A.48B.50C.98D.100
5.在数列{an}中,若a1=1,a2=3,an+2=an+1-an(n∈N*),则该数列的前100项之和是()
A.18B.8C.5D.2
6.已知等差数列{an}中,a3+a5=a4+7,a10=19,则数列{ancos nπ}的前2 024项和为()
A.1 011B.1 012C.2 022D.2 024
7.(多选)已知数列{an}的前n项和为Sn,a1=1,a2=2,且an+2-2an+1+an=0(n∈N*).记Tn=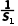 +
+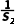 +…+
+…+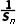 (n∈N*),则下列说法正确的是()
(n∈N*),则下列说法正确的是()
A.{an}为等差数列B.an=n+1C.Sn=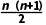 D.Tn=
D.Tn=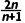
8.若数列{an}的通项公式是an= 其前n项和为Sn,则S30=.
其前n项和为Sn,则S30=.
9.数列1,3a,5a2,7a3,…,(2n-1)an-1,…(a≠0)的前n项和Sn=.
10.已知数列an=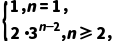 求数列{nan}的前n项和Tn.
求数列{nan}的前n项和Tn.
11.已知数列{an}是公比不为1的等比数列,且a3+a4=12,3a1,2a2,a3成等差数列.
(1)求an;
(2)设bn= 求数列{bn}的前2n项的和S2n.
求数列{bn}的前2n项的和S2n.
12.已知公差不为零的等差数列{an}的前n项和为Sn,若S5=30,且a1,a2,a4成等比数列.
(1)求数列{an}的通项公式;
(2)若bn=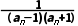 {bn}的前n项和Tn.
{bn}的前n项和Tn.
13.已知等比数列{an}的公比q>1,且a3+a5=40,a4=16.
(1)求数列{an}的通项公式;
(2)设bn=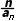 n是数列{bn}的前n项和,对任意正整数n,不等式Sn+
n是数列{bn}的前n项和,对任意正整数n,不等式Sn+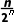 >(-1)n·a恒成立,求a的取值范围.
>(-1)n·a恒成立,求a的取值范围.