

第二章 直线和圆的方程
2.1 直线的倾斜角与斜率
2.1.1 倾斜角与斜率
新课程标准解读 | 核心素养 |
1.在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素 | 数学抽象 |
2.理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程,掌握过两点的直线斜率的计算公式 | 直观想象、 数学运算 |


经过平面直角坐标系中的一点,可以有无数条不同的直线.
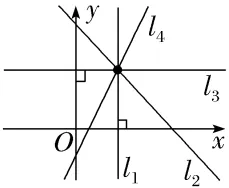
【问题】如图所示,过同一点的直线l1,l2,l3,l4,它们彼此之间的不同点是什么?你能找到一个量来描述它们的不同点吗?你找到的量,能够使得图中任意两条不同的直线都有不同的取值吗?

知识点一直线的倾斜角
1.定义:
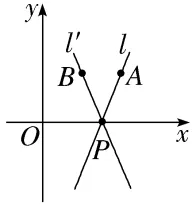
当直线l与x轴相交时,我们以x轴为基准,x轴 正向 与直线l 向上 的方向之间所成的角α叫做直线l的倾斜角.如图所示,直线l的倾斜角是∠APx,直线l'的倾斜角是∠BPx.
2.范围:直线的倾斜角α的取值范围为0°≤α<180° ,并规定当直线l与x轴平行或重合时,它的倾斜角为0°.
提醒在倾斜角的定义中,要注意三个条件:①直线向上的方向;②x轴的正向;③小于平角的非负角.
知识点二直线的斜率
1.定义:一条直线的倾斜角α的 正切 值叫做这条直线的斜率.斜率常用小写字母k表示,即k=tan α.
2.斜率公式:经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式为k=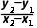 .当x1=x2时,直线P1P2没有斜率.
.当x1=x2时,直线P1P2没有斜率.
【想一想】
1.任何一条直线都有倾斜角吗?任何一条直线都有斜率吗?
提示:任何一条直线都有倾斜角.但倾斜角为90°的直线没有斜率.
2.直线的倾斜角越大,斜率就越大吗?
提示:不是,如60°<120°,但斜率分别为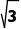 和-
和-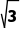
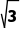 >-
>-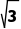 .应分区间说明,当α∈[0°,90°)和α∈(90°,180°)时,上述结论在这两个区间分别成立.
.应分区间说明,当α∈[0°,90°)和α∈(90°,180°)时,上述结论在这两个区间分别成立.
知识点三直线的方向向量
设P1(x1,y1),P2(x2,y2)(x1≠x2)是直线l上的两点,则向量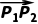 =(x2-x1,y2-y1)以及与它平行的向量都是直线的 方向向量 .若直线l的斜率为k,它的一个方向向量的坐标为(x,y),则k=
=(x2-x1,y2-y1)以及与它平行的向量都是直线的 方向向量 .若直线l的斜率为k,它的一个方向向量的坐标为(x,y),则k=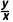 .
.

1.判断正误.(正确的画“√”,错误的画“×”)
(1)若α是直线l的倾斜角,则0°≤α≤180°.(×)
(2)若k是直线的斜率,则k∈R.(√)
(3)经过两点的直线的斜率公式适用于任何直线.(×)
2.已知直线l的倾斜角为30°,则直线l的斜率为()
A.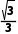 B.
B.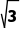
C.1D.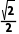
解析:A由题意可知,直线l的斜率k=tan 30°=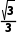 .
.
3.过点P(2,1),Q(4,5)的直线斜率为()
A.1B.2
C.3D.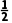
解析:B直线的斜率k=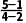 =2,故选B.
=2,故选B.
4.已知直线l的一方向向量为(1,),则直线l的倾斜角为60°.
解析:∵直线l的斜率k=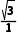 =
=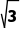 tan α=
tan α=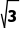 0°≤α<180°,故直线l的倾斜角为60°.
0°≤α<180°,故直线l的倾斜角为60°.

【例1】(1)若直线l向上的方向与y轴正向之间所成的角为30°,则直线l的倾斜角为(D)
A.30°B.60°
C.30°或150°D.60°或120°
解析:如图,直线l有两种情况,故l的倾斜角为60°或120°.
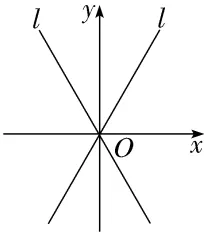
(2)已知直线l经过第二、四象限,则直线l的倾斜角α的取值范围是(C)
A.0°≤α<90°B.90°≤α<180°
C.90°<α<180°D.0°<α<180°
解析:直线的倾斜角的取值范围是0°≤α<180°,又直线l经过第二、四象限,所以直线l的倾斜角α的取值范围是90°<α<180°.
通性通法
直线倾斜角的求法及注意点
(1)直线的倾斜角主要根据定义来求,其关键是根据题意画出图形,找准倾斜角,有时要根据情况分类讨论;
(2)注意倾斜角的范围.
【跟踪训练】
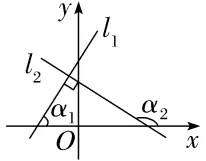
1.(2024·丽水月考)已知直线l1的倾斜角α1=60°,直线l2与l1垂直,则直线l2的倾斜角α2为()
A.30°B.60°
C.120°D.150°
解析:D画出示意图如图所示.因为直线l2与l1垂直,所以α2=α1+90°=150°,即直线l2的倾斜角为150°.
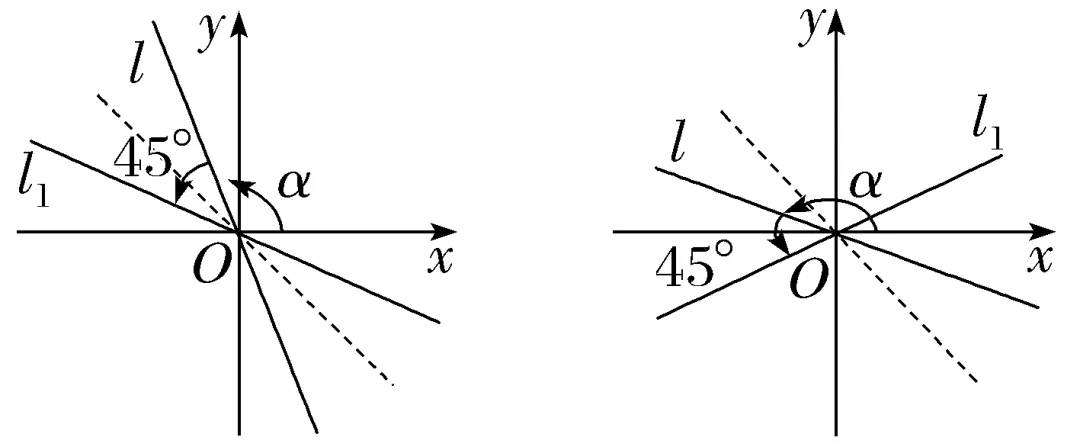
2.(多选)设直线l过坐标原点,它的倾斜角为α,如果将l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么l1的倾斜角可能为()
A.α+45°B.α-135°
C.135°-αD.α-45°
解析:AB根据题意,画出图形,如图所示,通过图象可知:当0°≤α<135°,l1的倾斜角为α+45°;当135°≤α<180°时,l1的倾斜角为45°+α-180°=α-135°.
【例2】(2024·江门质检)经过下列两点的直线的斜率是否存在?如果存在,求其斜率,并指出直线的倾斜角α.
(1)A(2,3),B(4,5);
解:(1)存在.直线AB的斜率kAB=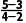 =1,即tan α=1,又0°≤α<180°,所以倾斜角α=45°.
=1,即tan α=1,又0°≤α<180°,所以倾斜角α=45°.
(2)C(-2,3),D(2,-1);
(2)存在.直线CD的斜率kCD=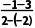 =-1,即tan α=-1,又0°≤α<180°,所以倾斜角α=135°.
=-1,即tan α=-1,又0°≤α<180°,所以倾斜角α=135°.
(3)P(a,2),Q(3,6).
(3)当a=3时,斜率不存在,直线的倾斜角为90°;当a≠3时,直线的斜率k=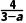 且倾斜角α满足tan α=
且倾斜角α满足tan α=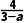 .
.
通性通法
解决斜率问题的方法
(1)由倾斜角(范围)求斜率(范围),利用定义式k=tan α(α≠90°)解决;
(2)由两点坐标求斜率,运用两点斜率公式k=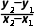 (x1≠x2)求解.
(x1≠x2)求解.
【跟踪训练】
1.已知过两点A(4,y),B(2,-3)的直线的倾斜角为135°,则y=-5.
解析:直线AB的斜率k=tan 135°=-1,又k=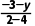
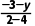 =-1,得y=-5.
=-1,得y=-5.
2.(2024·阳江月考)直线l1经过两点A(0,0),B(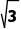 ),直线l2的倾斜角是直线l1的倾斜角的2倍,则l2的斜率为
),直线l2的倾斜角是直线l1的倾斜角的2倍,则l2的斜率为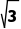 .
.
解析:因为直线l1的斜率为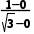 =
=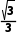 l1的倾斜角为
l1的倾斜角为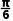 .又因为直线l2的倾斜角是直线l1的倾斜角的2倍,所以直线l2的倾斜角为
.又因为直线l2的倾斜角是直线l1的倾斜角的2倍,所以直线l2的倾斜角为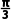 tan
tan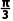 =
=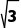 .
.
【例3】(1)若A(-2,3),B(m,-2),C(4,-3)三点共线,则实数m=3;
解析:因为A(-2,3),B(m,-2),C(4,-3)三点共线,且kAB=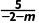 AC=
AC=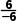 =-1,所以直线AB,AC的斜率存在,且kAB=kAC,即
=-1,所以直线AB,AC的斜率存在,且kAB=kAC,即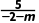 =-1,解得m=3.
=-1,解得m=3.
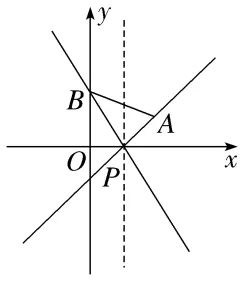
(2)直线l过点P(1,0),且与以A(2,1),B(0,)为端点的线段有公共点,则直线l的斜率的范围为(-∞,-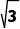 ]∪[1,+∞) ,倾斜角的范围为
]∪[1,+∞) ,倾斜角的范围为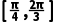 .
.
解析:如图所示.因为kAP=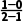 =1,kBP=
=1,kBP=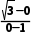 =-
=-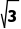 .所以k∈(-∞,-
.所以k∈(-∞,-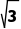 ]∪[1,+∞).所以
]∪[1,+∞).所以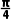 ≤α≤
≤α≤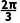 .
.
通性通法
1.用斜率公式解决三点共线的方法

2.求代数式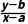 最值或范围的方法
最值或范围的方法
由斜率公式k=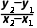 的形式,可知代数式
的形式,可知代数式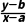 的几何意义是过P(x,y)与P'(a,b)两点的直线的斜率.故可以利用数形结合来求解.
的几何意义是过P(x,y)与P'(a,b)两点的直线的斜率.故可以利用数形结合来求解.
【跟踪训练】
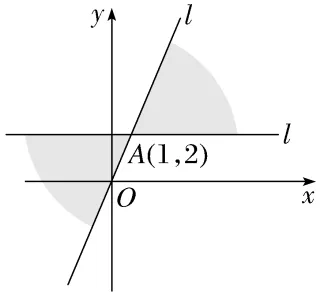
(2024·安阳月考)已知直线l经过点A(1,2),且不经过第四象限,则直线l的斜率k的取值范围是()
A.(-1,0]B.[0,1]
C.[1,2]D.[0,2]
解析:D如图,当直线l位于如图阴影部分所示的区域内时,满足题意,所以直线l的斜率满足0≤k≤2.故选D.

1.(2024·宿迁质检)图中α能表示直线l的倾斜角的是()
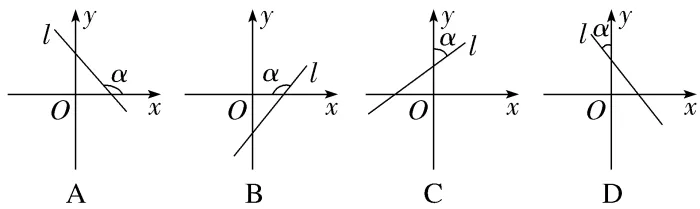
解析:A结合直线l的倾斜角的定义可知A可以.
2.下面选项中,两点确定的直线的斜率不存在的是()
A.(4,2)与(-4,1)B.(0,3)与(3,0)
C.(3,-1)与(2,-1)D.(-2,2)与(-2,5)
解析:DD项,因为x1=x2=-2,所以直线垂直于x轴,倾斜角为90°,斜率不存在.
3.过A(4,y),B(2,-3)两点的直线的一个方向向量为n=(-1,-1),则y=()
A.-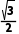 B.
B.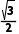
C.-1D.1
解析:C法一由直线的方向向量为n=(-1,-1),得直线的斜率为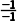 =1,所以
=1,所以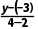 =1,解得y=-1.
=1,解得y=-1.
法二由题意得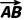 =(-2,-3-y).又直线AB的一个方向向量为n=(-1,-1),所以n∥
=(-2,-3-y).又直线AB的一个方向向量为n=(-1,-1),所以n∥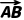 (-2)×(-1)-(-3-y)×(-1)=0,解得y=-1.
(-2)×(-1)-(-3-y)×(-1)=0,解得y=-1.


1.给出下列命题,其中为真命题的是()
A.任意一条直线都有唯一的倾斜角
B.一条直线的倾斜角可以为-30°
C.倾斜角为0°的直线只有一条,即x轴
D.若α是直线l的倾斜角,且sin α=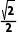 α=45°
α=45°
解析:A任意一条直线都有唯一的倾斜角,倾斜角不可能为负,倾斜角为0°的直线有无数条,它们都垂直于y轴,因此A正确,B、C错误.D中α有可能为135°,故D错误.
2.若直线过坐标平面内两点(4,2),(1,2+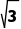 ),则此直线的倾斜角是()
),则此直线的倾斜角是()
A.30°B.150°
C.60°D.120°
解析:B由题意知k=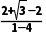 =-
=-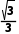 直线的倾斜角为150°.
直线的倾斜角为150°.
3.若经过A(m,3),B(1,2)两点的直线的倾斜角为45°,则m=()
A.2B.1
C.-1D.-2
解析:A由题意知,tan 45°=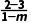 m=2.
m=2.
4.(2024·佛山月考)已知直线PQ的斜率为-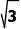 PQ绕点P顺时针旋转60°,所得的直线的斜率是()
PQ绕点P顺时针旋转60°,所得的直线的斜率是()
A.0B.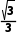
C.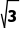 D.-
D.-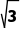
解析:C由题意,知直线PQ的倾斜角为120°,直线PQ绕点P顺时针旋转60°,所得直线的倾斜角为60°,所以斜率为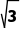 .
.
5.“直线l的斜率不小于0”是“直线l的倾斜角为锐角”的()
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
解析:B若直线l的斜率不小于0,则该直线的倾斜角为锐角或0°,若直线l的倾斜角为锐角,则该直线l的斜率为正数,即大于0,所以“直线l的斜率不小于0”是“直线l的倾斜角为锐角”的必要不充分条件.故选B.
6.(多选)已知点A的坐标为(3,4),在坐标轴上有一点B,若kAB=4,则点B的坐标可能为()
A.(0,-4)B.(4,0)
C.(2,0)D.(0,-8)
解析:CD设B(x,0)或(0,y),因为kAB=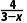 或kAB=
或kAB=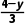
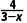 =4或
=4或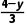 =4,所以x=2或y=-8,所以点B的坐标为(2,0)或(0,-8).
=4,所以x=2或y=-8,所以点B的坐标为(2,0)或(0,-8).
7.(2024·南平月考)已知点A(m,-m+3),B(2,m-1),C(-1,4),直线AC的斜率等于直线BC的斜率的3倍,则m=4.
解析:由题意知直线AC的斜率存在,即m≠-1.所以kAC=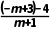 BC=
BC=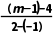 .所以
.所以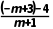 =3×
=3×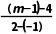 .整理,得-m-1=(m-5)(m+1),即(m+1)(m-4)=0.解得m=4或m=-1(舍去).所以m=4.
.整理,得-m-1=(m-5)(m+1),即(m+1)(m-4)=0.解得m=4或m=-1(舍去).所以m=4.
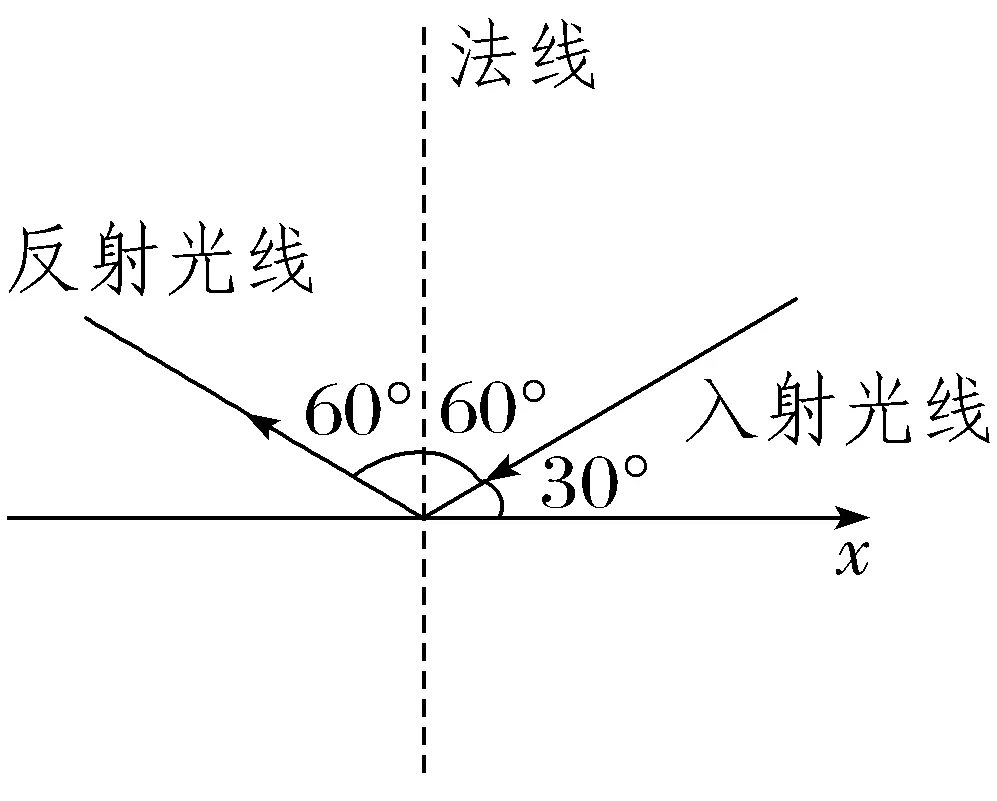
8.一束光线射到x轴上并经x轴反射,已知入射光线的倾斜角α1=30°,则反射光线的倾斜角α2=150°.
解析:作出入射光线和反射光线,如图.因为入射光线的倾斜角α1=30°,所以入射角为60°.又反射角等于入射角,由图易知,反射光线的倾斜角为60°+60°+30°=150°.
9.(2024·福州质检)如图,已知直线l1的倾斜角是150°,l2⊥l1,垂足为B.l1,l2与x轴分别相交于点C,A,l3平分∠BAC,则l3的倾斜角为30°.
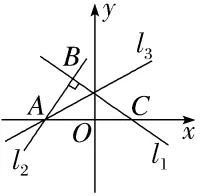
解析:因为直线l1的倾斜角为150°,所以∠BCA=30°,所以l3的倾斜角为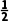 ×(90°-30°)=30°.
×(90°-30°)=30°.
10.已知直线l经过两点A(-1,m),B(m,1),问:当m取何值时:
(1)直线l与x轴平行?
解:若直线l与x轴平行,则直线l的斜率k=0,所以m=1.
(2)直线l的方向向量的坐标为(3,1).
解:直线l的方向向量的坐标为(3,1),故k=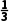
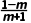 =
=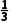 m=
m=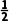 .
.
(3)直线的倾斜角为45°?
解:由题意可知,直线l的斜率k=1,即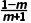 =1, 解得m=0.
=1, 解得m=0.

11.(2024·重庆质检)斜拉桥是桥梁建筑的一种形式,在桥梁平面上有多根拉索,所有拉索的合力方向与中央索塔一致.重庆千厮门嘉陵江大桥如图①所示,桥上共有10对永久拉索,在索塔两侧对称排列,示意图如图②所示.已知拉索上端相邻两个锚的间距|PiPi+1|(i=1,2,3,…,9)均为3.4 m,拉索下端相邻两个锚的间距|AiAi+1|(i=1,2,3,…,9)均为16 m.最短拉索的锚P1,A1满足|OP1|=66 m,|OA1|=86 m,则最长拉索所在直线的斜率为()

A.±0.47B.±0.45
C.±0.42D.±0.40
解析:C根据题意,得|OA10|=|OA1|+|A1A10|=86+9×16=230 m,|OP10|=|OP1|+|P1P10|=66+9×3.4=96.6 m.则右侧最长拉索所在直线的斜率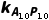 =-tan∠OA10P10=-
=-tan∠OA10P10=-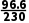 =-0.42,同理,左侧最长拉索所在直线的斜率
=-0.42,同理,左侧最长拉索所在直线的斜率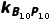 =0.42.故选C.
=0.42.故选C.
12.(多选)如图,直线l1,l2,l3的斜率分别为k1,k2,k3,倾斜角分别为α1,α2,α3,则下列选项正确的是()
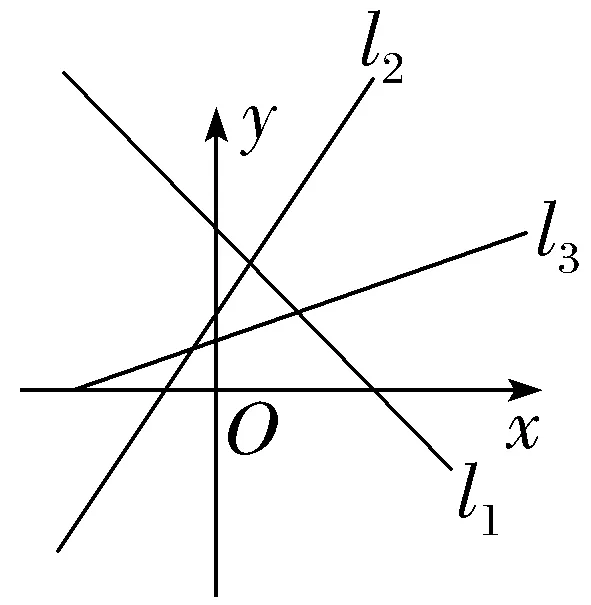
A.k1<k3<k2B.k3<k2<k1
C.α1<α3<α2D.α3<α2<α1
解析:AD由题图可知k2>k3>0,k1<0,故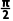 >α2>α3>0,且α1为钝角,即k1<k3<k2,α3<α2<α1,故选A、D.
>α2>α3>0,且α1为钝角,即k1<k3<k2,α3<α2<α1,故选A、D.
13.过点M(0,1)和N(1,m2+1)(m∈R)的直线的倾斜角的范围是[0,).
解析:由题意知,直线MN的斜率为k=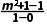 =m2≥0.设直线MN的倾斜角为θ,则tan θ≥0.又θ∈[0,π),所以θ∈[0,).
=m2≥0.设直线MN的倾斜角为θ,则tan θ≥0.又θ∈[0,π),所以θ∈[0,).
14.(2024·南阳质检)已知A(1,2),B(2,1),C(0,m)三点.
(1)若过A,C两点的直线的倾斜角为45°,求m的值;
解:过A,C两点的直线的斜率为kAC=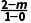 =2-m,
=2-m,
又直线AC的倾斜角为45°,
所以kAC=tan 45°=1=2-m,解得m=1.
(2)A,B,C三点可能共线吗?若能,求出m的值;若不能,请说明理由.
解:能.由题意知kAC=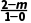 =2-m,kAB=
=2-m,kAB=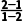 =-1.
=-1.
若A,B,C三点共线,则有kAB=kAC,即-1=2-m,
解得m=3,所以A,B,C三点能共线,且m=3.

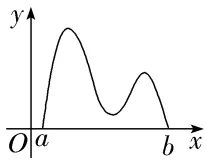
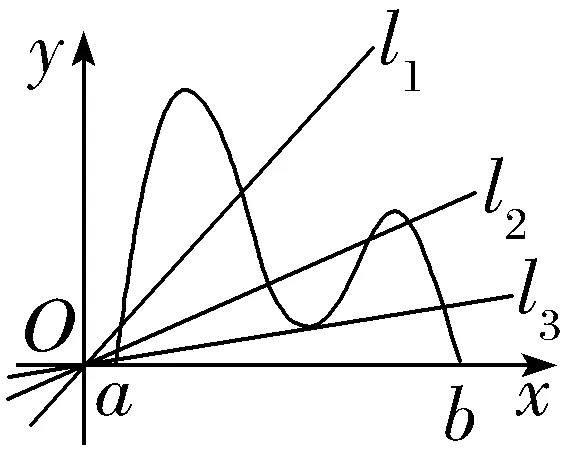
15.(2024·泉州月考)函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…,xn,使得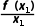 =
=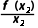 =…=
=…=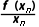 n的取值范围是()
n的取值范围是()
A.{3,4}B.{2,3,4}
C.{3,4,5}D.{2,3}
解析:B由题意,函数y=f(x)的图象上的任一点坐标为(x,f(x)),故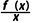 表示曲线上任一点与坐标原点连线的斜率.若
表示曲线上任一点与坐标原点连线的斜率.若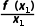 =
=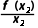 =…=
=…=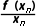 n个点与原点连线的斜率相等,即过原点的直线与曲线y=f(x)有n个交点.如图,数形结合可得n的取值可为2,3,4.
n个点与原点连线的斜率相等,即过原点的直线与曲线y=f(x)有n个交点.如图,数形结合可得n的取值可为2,3,4.
16.已知坐标平面内三点A(-1,1),B(1,1),C(2,+1).
(1)求直线AB,BC,AC的斜率和倾斜角;
(2)若D为△ABC的边AB上一动点,求直线CD的斜率k的取值范围.
解:(1)由斜率公式得kAB=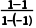 =0,
=0,
kBC=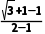 =
=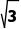 AC=
AC=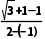 =
=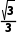 .
.
又倾斜角的取值在[0°,180°)范围内,
∵tan 0°=0,∴直线AB的倾斜角为0°.
∵tan 60°=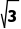 直线BC的倾斜角为60°.
直线BC的倾斜角为60°.
∵tan 30°=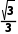 直线AC的倾斜角为30°.
直线AC的倾斜角为30°.
(2)如图,直线CD绕点C旋转,当直线CD由CA逆时针转到CB时,
直线CD与AB恒有交点,即D在线段AB上,此时k由kCA增大到kCB,∴k的取值范围为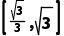 .
.
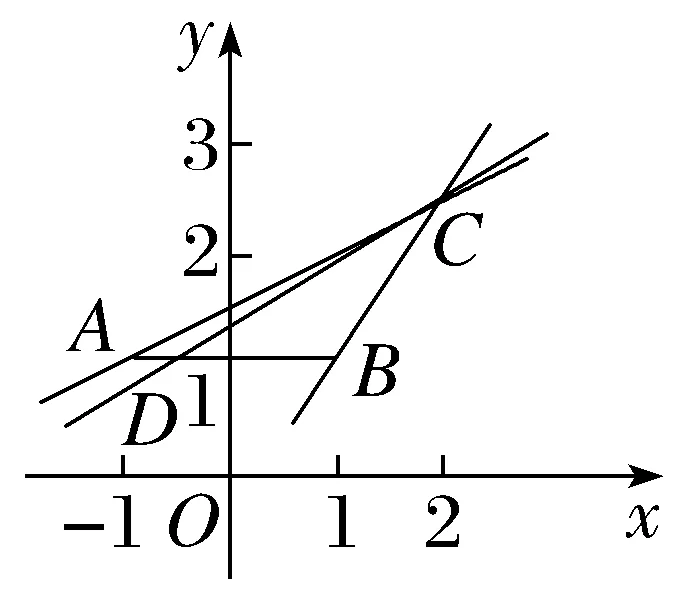

通过网盘分享的文件:25-26学年同步培优讲义
链接: https://pan.baidu.com/s/1y0bSGZE1YoJg8gMTXiqQoA?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享