

4.5.2用二分法求方程的近似解
新课程标准解读 | 核心素养 |
1.探索用二分法求方程近似解的思路并会画程序框图 | 数学抽象 |
2.能借助计算工具用二分法求方程的近似解 | 数学运算 |
3.了解用二分法求方程近似解具有一般性 | 数学运算、逻辑推理 |


电视台某栏目中有一个猜商品价格的游戏,规则如下:给出一种商品让参赛者猜价格,主持人给出提示语“高了”或“低了”.例如参赛者猜某种商品的价格为100元,主持人说“高了”.参赛者又猜50元,主持人说“低了”.参赛者再猜80元,主持人说“低了”.这样一直猜下去,直到猜中为止.
【问题】(1)我们怎么猜才能尽快猜中价格呢?
(2)这种思路能不能运用到求方程的近似解中呢?

知识点一二分法
条件 | (1)函数y=f(x)的图象在区间[a,b]上 连续不断 ; (2)在区间端点的函数值满足f(a)f(b)<0 |
方法 | 不断地把函数y=f(x)的零点所在区间 一分为二 ,使所得区间的两个端点逐步 逼近零点 ,进而得到零点近似值 |
提醒用二分法只能求变号零点,即零点左右两侧的函数值的符号相反,比如y=x2,该函数有零点为0,但不能用二分法求解.
知识点二 二分法求函数零点近似值的步骤

提醒二分法求函数零点近似值口诀
定区间,找中点,中值计算两边看;
同号去,异号算,零点落在异号间;
周而复始怎么办?精确度上来判断.

1.下列函数图象与x轴均有公共点,其中能用二分法求零点的是()
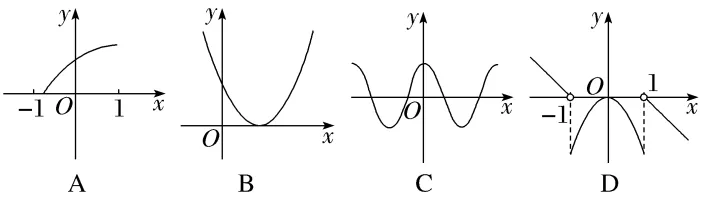
解析:C只有选项C中零点左右的函数值符号相反,且函数的图象连续不断,可以利用二分法求解.
2.用二分法研究函数f(x)=x3+3x-1的零点时,第一次经计算得f(0)<0,f(0.5)>0,可得其中一个零点x0∈(0,0.5) ,第二次应计算f(0.25).

【例1】(1)已知函数f(x)的图象如图所示,其中零点的个数与可以用二分法求解的个数分别为()
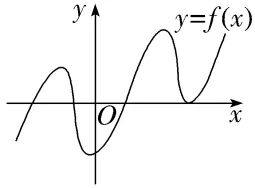
A.4,4B.3,4
C.5,4D.4,3
(2)(多选)下列函数中,能用二分法求函数零点的有()
A.f(x)=3x-1B.f(x)=x2-2x+1
C.f(x)=4xD.f(x)=ex-2
答案:(1)D(2)ACD
解析:(1)图象与x轴有4个交点,所以零点的个数为4;左右函数值异号的零点有3个,所以可以用二分法求解的个数为3,故选D.
(2)f(x)=x2-2x+1=(x-1)2,f(1)=0,当x<1时,f(x)>0;当x>1时,f(x)>0,在零点两侧函数值同号,不能用二分法求零点,其余选项中函数的零点两侧的函数值异号.故选A、C、D.
通性通法
二分法的适用条件
判断一个函数能否用二分法求其零点的依据是:其图象在零点附近是连续不断的,且该零点为变号零点.因此,用二分法求函数的零点近似值的方法仅对函数的变号零点适用,对函数的不变号零点不适用.
【跟踪训练】
在用二分法求函数f(x)零点的近似值时,第一次所取的区间是[-2,4],则第三次所取的区间可能是()
A.[1,4]B.[-2,1]
C.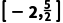 D.
D.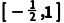
解析:D∵第一次所取的区间是[-2,4],∴第二次所取的区间可能为[-2,1],[1,4],∴第三次所取的区间可能为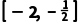 .
.
【例2】用二分法求方程2x3+3x-3=0的一个正实数近似解.(精确度为0.1)
解:令f(x)=2x3+3x-3,
经计算,f(0)=-3<0,f(1)=2>0,f(0)·f(1)<0,
所以函数f(x)在(0,1)内存在零点,
即方程2x3+3x-3=0在(0,1)内有解.
取(0,1)的中点0.5,经计算f(0.5)<0,
又f(1)>0,
所以方程2x3+3x-3=0在(0.5,1)内有解.
如此继续下去,得到方程的正实数根所在的区间,如表:
(a,b) | 中点c | f(a) | f(b) | f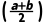 |
(0,1) | 0.5 | f(0)<0 | f(1)>0 | f(0.5)<0 |
(0.5,1) | 0.75 | f(0.5)<0 | f(1)>0 | f(0.75)>0 |
(0.5,0.75) | 0.625 | f(0.5)<0 | f(0.75)>0 | f(0.625)<0 |
(0.625,0.75) | 0.687 5 | f(0.625)<0 | f(0.75)>0 | f(0.687 5)<0 |
(0.687 5,0.75) | |0.687 5-0.75|=0.062 5<0.1 |
由于|0.6875-0.75|=0.0625<0.1,所以0.75可作为方程的一个正实数近似解.
【母题探究】
(变条件)若本例中的“精确度为0.1”换为“精确度为0.05”结论又如何?
解:在本例的基础上,取区间(0.6875,0.75)的中点x=0.71875,因为f(0.71875)<0,f(0.75)>0且|0.71875-0.75|=0.03125<0.05,所以x=0.72可作为方程的一个近似解.
通性通法
用二分法求函数零点的近似值应遵循的原则
(1)需依据图象估计零点所在的初始区间[m,n](一般采用估计值的方法完成);
(2)取区间端点的中点c,计算f(c),确定有解区间是(m,c)还是(c,n),逐步缩小区间的“长度”,直到区间的两个端点符合精确度要求,终止计算,得到函数零点的近似值.
【跟踪训练】
用二分法求方程x2-2x-1=0的正实数解的近似值.(精确度为0.1)
解:令f(x)=x2-2x-1,∵f(2)=-1<0,f(3)=2>0,
又∵f(x)在(2,3)上单调递增,
∴在(2,3)内方程x2-2x-1=0有唯一的实数解,记作x0.
取区间中点x1=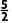 ,∵f(
,∵f(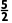 )=
)=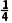 >0,∴x0∈(2,);
>0,∴x0∈(2,);
再取区间(2,)的中点x2=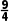 ,∵f(
,∵f(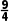 )=-
)=-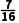 <0,∴x0∈(
<0,∴x0∈(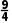 );
);
再取区间(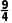 )的中点x3=
)的中点x3=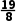 ,∵f(
,∵f(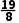 )=
)=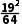 -
-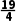 -1=-
-1=-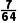 <0,∴x0∈(
<0,∴x0∈(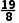 ),
),
此时
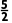 -
-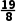
 =
=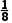 =0.125>0.1;
=0.125>0.1;
再取区间(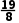 )的中点x4=
)的中点x4=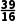 ,∵f(
,∵f(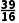 )=(
)=(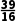 )2-2×
)2-2×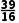 -1=
-1=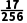 >0,∴x0∈(
>0,∴x0∈(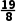 ),
),
此时
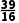 -
-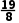
 =
=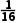 =0.0625<0.1且
=0.0625<0.1且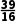 =2.4375.
=2.4375.
故方程x2-2x-1=0的正实数解的近似值可取为2.4.
【例3】在一个风雨交加的夜晚,从某水库闸门到防洪指挥所的电话线路发生了故障,这是一条长为10 km,大约有200根电线杆的线路,试用二分法思想设计一个能迅速查出故障所在的方案,维修线路的工人师傅至多检测几次就能找出故障地点所在区域(精确到100 m范围内)?
解:如图,工人师傅首先从中点C检测,用随身带的话机向两端测试,发现AC段正常,可见故障在BC段;再从线段BC的中点D检测,发现BD段正常,可见故障在CD段;再从CD段的中点E检测;…,由此类推,每查一次,可以把待查的线路长度缩减一半,可以算出经过n次检测,所剩线路的长度为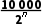 m,则有
m,则有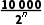 ≤100,即2n≥100,又26=64,27=128,故至多检测7次就能找到故障地点所在区域.
≤100,即2n≥100,又26=64,27=128,故至多检测7次就能找到故障地点所在区域.

通性通法
二分法的思想在实际生活中应用十分广泛,二分法不仅可用于线路、水管、煤气管道故障的排查,还能用于实验设计、资料查询、资金分配等.
【跟踪训练】
一块电路板的AB段之间有60个串联的焊接点,知道电路不通的原因是焊口脱落造成的,要想用二分法的思想检测出哪处焊口脱落,至多需要检测几次?
解:第一次,可去掉30个结果,从剩余的30个中继续二分法;
第二次,可去掉15个结果,从剩余的15个中继续二分法;
第三次,可去掉7或8个结果,考虑至多的情况,所以去掉7个结果,从剩余的8个中继续二分法;
第四次,可去掉4个结果,从剩余的4个中继续二分法;
第五次,可去掉2个结果,从剩余的2个中继续二分法;
第六次,可去掉1个结果,得到最终结果,所以至多需要检测六次.

1.下列函数图象中,不能用二分法求函数零点的是()
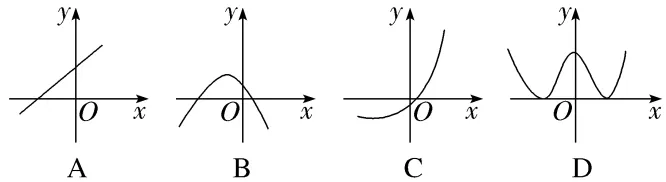
解析:D根据函数零点存在定理,对于D,在零点的左右附近,函数值不改变符号,所以不能用二分法求函数零点,故选D.
2.用二分法求函数f(x)=2x-3的零点时,初始区间可选为()
A.(-1,0)B.(0,1)
C.(1,2)D.(2,3)
解析:C f(-1)=-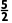 <0,f(0)=-2<0,f(1)=-1<0,f(2)=1>0,f(3)=5>0,则f(1)f(2)<0,即初始区间可选(1,2).
<0,f(0)=-2<0,f(1)=-1<0,f(2)=1>0,f(3)=5>0,则f(1)f(2)<0,即初始区间可选(1,2).
3.设f(x)=lg x+x-3,用二分法求方程lg x+x-3=0在(2,3)内近似解的过程中得f(2.25)<0,f(2.75)>0,f(2.5)<0,f(3)>0,则方程的根落在区间()
A.(2,2.25)B.(2.25,2.5)
C.(2.5,2.75)D.(2.75,3)
解析:C因为f(2.5)<0,f(2.75)>0,由零点存在定理知,方程的根在区间(2.5,2.75)内,故选C.
4.若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:
f(1)=-2 | f(1.5)=0.625 |
f(1.25)=-0.984 | f(1.375)=-0.260 |
f(1.438)=0.165 | f(1.406 5)=-0.052 |
那么方程x3+x2-2x-2=0的一个近似根(精确度为0.05)为()
A.1.5B.1.375
C.1.438D.1.25
解析:C∵f(1.4065)<0,f(1.438)>0,∴f(1.4065)·f(1.438)<0,∴该方程的根在区间(1.4065,1.438)内,又∵|1.4065-1.438|=0.0315<0.05,∴方程的近似根可以是1.438.


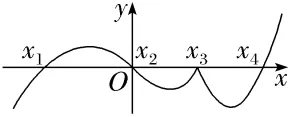
1.用二分法求如图所示的函数f(x)的零点时,不可能求出的零点是()
A.x1B.x2
C.x3D.x4
解析:C能用二分法求零点的函数必须满足在区间[a,b]上连续不断,且f(a)f(b)<0.而x3左右两侧的函数值都小于零,不满足区间端点处函数值符号相异的条件.
2.用二分法求函数f(x)在(a,b)内的唯一零点时,精确度为0.001,则结束计算的条件是()
A.|a-b|<0.1B.|a-b|<0.001
C.|a-b|>0.001D.|a-b|=0.001
解析:B根据二分法的步骤知当|b-a|小于精确度ε时,便可结束计算.
3.若函数f(x)在[a,b]上的图象为一条连续不断的曲线,且同时满足f(a)·f(b)<0,f(a)·f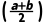 >0,则()
>0,则()
A.f(x)在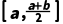 上有零点
上有零点
B.f(x)在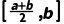 上有零点
上有零点
C.f(x)在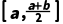 上无零点
上无零点
D.f(x)在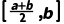 上无零点
上无零点
解析:B由f(a)·f(b)<0,f(a)·f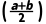 >0可知f
>0可知f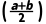 ·f(b)<0,根据函数零点存在定理可知f(x)在
·f(b)<0,根据函数零点存在定理可知f(x)在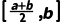 上有零点.
上有零点.
4.用二分法求方程的近似解,求得f(x)=x3+2x-9的部分函数值数据如表所示:
x | 1 | 2 | 1.5 | 1.625 | 1.75 | 1.875 | 1.812 5 |
f(x) | -6 | 3 | -2.625 | -1.459 | -0.14 | 1.341 8 | 0.579 3 |
则当精确度为0.1时,方程x3+2x-9=0的近似解可取为()
A.1.6B.1.7
C.1.8D.1.9
解析:C由表格可得,函数f(x)=x3+2x-9的零点在区间(1.75,1.8125)内.结合选项可知,方程x3+2x-9=0的近似解可取为1.8.故选C.
5.(多选)下列关于函数f(x),x∈[a,b]的命题中,不正确的是()
A.若x0∈[a,b]且满足f(x0)=0,则x0是f(x)的一个零点
B.若x0是f(x) 在[a,b]上的零点,则可以用二分法求x0的近似值
C.函数f(x)的零点是方程f(x)=0的根,但f(x)=0的根不一定是函数f(x)的零点
D.用二分法求方程的根时,得到的都是近似解
解析:BCD使用“二分法”必须满足“二分法”的使用条件,B不正确;f(x)=0的根也一定是函数f(x)的零点,C不正确;用二分法求方程的根时,得到的也可能是精确解,D不正确,只有A正确.
6.(多选)在用二分法求函数f(x)的一个正实数零点时,经计算,f(0.64)<0,f(0.72)>0,f(0.68)<0,则函数的一个精确度为0.05的正实数零点的近似值可以为()
A.0.68B.0.72
C.0.7D.0.6
解析:ABC已知f(0.64)<0,f(0.72)>0,则函数f(x)的零点的初始区间为(0.64,0.72),又因为0.68=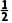 ×(0.64+0.72),且f(0.68)<0,所以零点在区间(0.68,0.72)上,|0.72-0.68|=0.04<0.05,所以0.68,0.7,0.72都符合.
×(0.64+0.72),且f(0.68)<0,所以零点在区间(0.68,0.72)上,|0.72-0.68|=0.04<0.05,所以0.68,0.7,0.72都符合.
7.函数f(x)=x2+ax+b有零点,但不能用二分法求出,则a,b的关系是a2=4b.
解析:∵函数f(x)=x2+ax+b有零点,但不能用二分法求出,∴函数f(x)=x2+ax+b的图象与x轴相切,∴Δ=a2-4b=0,∴a2=4b.
8.用二分法求方程ln x-2+x=0在区间[1,2]上零点的近似值,先取区间中点c=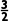
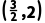 .
.
解析:令f(x)=lnx-2+x,∵f(1)=-1<0,f(2)=ln2>0,f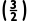 =ln
=ln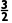 -
-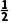 <0,∴下一个含根的区间是
<0,∴下一个含根的区间是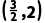 .
.
9.在12枚崭新的硬币中,有一枚外表与真币完全相同的假币(质量小一点),现在只有一台天平,则应用二分法的思想,最多称 3 次就可以发现假币.
解析:将12枚硬币平均分成两份,放在天平上,假币在轻的那6枚硬币里面;将这6枚平均分成两份,则假币一定在轻的那3枚硬币里面;将这3枚硬币任拿出2枚放在天平上,若平衡,则剩下的那一枚即是假币;若不平衡,则轻的那一枚即是假币,依据上述分析,最多称3次就可以发现这枚假币.
10.已知方程2x+2x=5.
(1)判断该方程解的个数以及所在区间;
(2)用二分法求出方程的近似解(精确度为0.1).
参考数值:
x | 1.25 | 1.281 25 | 1.312 5 | 1.375 | 1.5 |
2x | 2.378 | 2.430 | 2.484 | 2.594 | 2.828 |
解:(1)令f(x)=2x+2x-5.
因为函数f(x)=2x+2x-5在R上是增函数,所以函数f(x)=2x+2x-5至多有一个零点.
因为f(1)=21+2×1-5=-1<0,
f(2)=22+2×2-5=3>0,
所以方程2x+2x=5有一解在(1,2)内.
(2)用二分法逐次计算,列表如下:
区间 | 中点的值 | 中点函数值符号 |
(1,2) | 1.5 | f(1.5)>0 |
(1,1.5) | 1.25 | f(1.25)<0 |
(1.25,1.5) | 1.375 | f(1.375)>0 |
(1.25,1.375) | 1.3125 | f(1.3125)>0 |
(1.25,1.3125) | 1.28125 | f(1.28125)<0 |
因为|1.375-1.25|=0.125>0.1,
且|1.3125-1.25|=0.0625<0.1,
所以函数零点的近似值可取为1.3125,
即方程2x+2x=5的近似解可取为1.3125.

11.用二分法求方程x-2lg 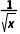 =3的近似解,可以取的一个区间是()
=3的近似解,可以取的一个区间是()
A.(0,1)B.(1,2)
C.(2,3)D.(3,4)
解析:C令f(x)=x-2lg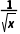 -3,则f(2)=2-2lg
-3,则f(2)=2-2lg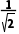 -3=2-2×(-
-3=2-2×(-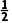 )lg2-3=lg2-1<0,f(3)=3-3lg
)lg2-3=lg2-1<0,f(3)=3-3lg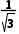 -3=
-3=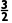 lg3>0,∴用二分法求方程x-2lg
lg3>0,∴用二分法求方程x-2lg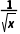 =3的近似解,可以取的一个区间是(2,3).
=3的近似解,可以取的一个区间是(2,3).
12.用二分法求函数f(x)=ln(x+1)+x-1在区间(0,1)上的零点,要求精确度为0.01时,所需二分区间的次数最少为()
A.5B.6
C.7D.8
解析:C开区间(0,1)的长度等于1,每经过一次操作,区间长度变为原来的一半,经过n次操作后,区间长度变为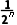 .因为精确度为0.01,所以
.因为精确度为0.01,所以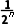 <0.01.又n∈N*,所以n≥7且n∈N*,故所需二分区间的次数最少为7,故选C.
<0.01.又n∈N*,所以n≥7且n∈N*,故所需二分区间的次数最少为7,故选C.
13.某同学在借助计算器求“方程lg x=2-x的近似解(精确度为0.1)”时,设f(x)=lg x+x-2,算得f(1)<0,f(2)>0;在以下过程中,他用“二分法”又取了4个x的值,计算了其函数值的正负,并得出判断:方程的近似解是x≈1.8.那么他再取的x的4个值依次是 1.5,1.75,1.875,1.812 5 .
解析:第一次用二分法计算得区间(1.5,2),第二次得区间(1.75,2),第三次得区间(1.75,1.875),第四次得区间(1.75,1.8125).
14.已知函数f(x)=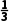 x3-x2+1.
x3-x2+1.
(1)证明方程f(x)=0在区间(0,2)内有实数解;
(2)使用二分法,取区间的中点三次,指出方程f(x)=0(x∈[0,2])的实数解x0在哪个较小的区间内.
解:(1)证明:因为f(0)=1>0,f(2)=-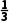 <0,所以f(0)·f(2)<0,由函数零点存在定理可得方程f(x)=0在区间(0,2)内有实数解.
<0,所以f(0)·f(2)<0,由函数零点存在定理可得方程f(x)=0在区间(0,2)内有实数解.
(2)取x1=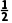 ×(0+2)=1,得f(1)=
×(0+2)=1,得f(1)=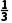 >0,
>0,
由此可得f(1)·f(2)<0,下一个有解区间为(1,2).
再取x2=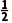 ×(1+2)=
×(1+2)=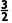 f
f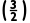 =-
=-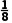 <0,
<0,
所以f(1)·f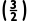 <0,下一个有解区间为
<0,下一个有解区间为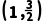 .
.
再取x3=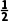 ×
×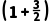 =
=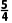 f
f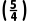 =
=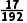 >0,
>0,
所以f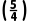 ·f
·f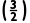 <0,下一个有解区间为
<0,下一个有解区间为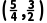 .
.
综上所述,所求的实数解x0在区间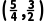 内.
内.

15.已知定义在区间[a,b]上的增函数f(x),在用二分法寻找零点的过程中,依次确定了零点所在区间为[a,b],[a,],[a+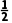 ],又f(
],又f(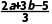 )=0,则函数f(x)的零点为()
)=0,则函数f(x)的零点为()
A.-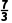 B.-
B.-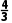
C.-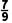 D.-
D.-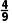
解析:C由题意得,f(a)<0,f(b)>0,又a+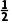 >a恒成立,则
>a恒成立,则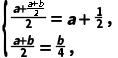 解得
解得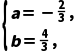 ∵f(
∵f(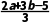 )=0,∴f(x)的零点为
)=0,∴f(x)的零点为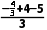 =-
=-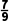 .故选C.
.故选C.
16.已知函数f(x)=2x2-8x+m+3为R上的连续函数.
(1)若m=-4,判断f(x)在(-1,1)上是否有零点.若没有,请说明理由;若有,请在精确度为0.2的条件下,用二分法求出这个零点x0所在的区间;
(2)若函数f(x)在区间[-1,1]上存在零点,求实数m的取值范围.
解:(1)m=-4时,f(x)=2x2-8x-1,
∴f(-1)=9,f(1)=-7,则f(-1)f(1)<0,
∵f(x)为R上的连续函数,
∴f(x)在(-1,1)上必有零点x0,
取其中点0,代入函数解析式得f(0)=-1<0,
∴f(-1)f(0)<0,∴零点x0∈(-1,0),
再取中点-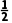 f(-
f(-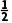 )=
)=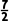 >0,
>0,
∴f(0)f(-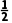 )<0,
)<0,
∴零点x0∈(-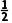 ),
),
取其中点-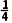 f(-
f(-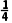 )=
)=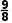 >0,
>0,
∴f(0)f(-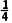 )<0,∴零点x0∈(-
)<0,∴零点x0∈(-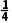 ),
),
再取其中点-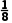 f(-
f(-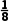 )=
)=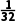 >0,
>0,
∴f(0)f(-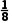 )<0,
)<0,
∴零点x0∈(-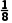 ),又
),又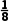 <
<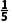
∴符合要求,故在精确度为0.2的条件下,零点x0所在的区间为(-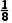 ).
).
(2)f(x)=2x2-8x+m+3的图象开口向上,对称轴为直线x=-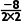 =2,∴在区间[-1,1]上,函数f(x)单调递减,又f(x)在区间[-1,1]上存在零点,
=2,∴在区间[-1,1]上,函数f(x)单调递减,又f(x)在区间[-1,1]上存在零点,
∴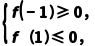 即
即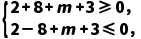
∴-13≤m≤3,即m的取值范围是[-13,3].

通过网盘分享的文件:25-26学年同步培优讲义
链接: https://pan.baidu.com/s/1y0bSGZE1YoJg8gMTXiqQoA?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享