

第2课时函数单调性的应用

【例1】讨论函数f(x)=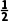 ax2+x-(a+1)ln x(a≥0)的单调性.
ax2+x-(a+1)ln x(a≥0)的单调性.
解:函数f(x)的定义域为(0,+∞),
f'(x)=ax+1-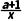 =
=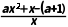 .
.
①当a=0时,f'(x)=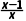
由f'(x)>0,得x>1,
由f'(x)<0,得0<x<1.
∴f(x)在(0,1)内单调递减,在(1,+∞)内单调递增.
②当a>0时,f'(x)=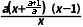
∵a>0,∴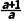 >0.
>0.
由f'(x)>0,得x>1,由f'(x)<0,得0<x<1.
∴f(x)在(0,1)内单调递减,在(1,+∞)内单调递增.
综上所述,当a≥0时,f(x)在(0,1)内单调递减,在(1,+∞)内单调递增.
通性通法
讨论含参函数的单调性的关键点
(1)涉及含参数的函数的单调性问题,一定要判断参数对导数f'(x)在某一个区间内的正负是否有影响.若有影响,则必须分类讨论,讨论时要做到不重不漏,最后进行总结;
(2)求含参函数y=f(x)的单调区间,实质上就是解含参数的不等式f'(x)>0,f'(x)<0.
【跟踪训练】
设函数f(x)=ex-ax-2(a∈R),求f(x)的单调区间.
解:f(x)的定义域为(-∞,+∞),f'(x)=ex-a.
若a≤0,则f'(x)>0,
所以f(x)在(-∞,+∞)上是增函数.
若a>0,则当x∈(-∞,lna)时,f'(x)<0;
当x∈(lna,+∞)时,f'(x)>0.
所以f(x)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增.
综上所述,当a≤0时,函数f(x)在(-∞,+∞)上是增函数;
当a>0时,f(x)的单调递减区间为(-∞,lna),
单调递增区间为(lna,+∞).
【例2】已知函数f(x)=x3-ax-1为R上的增函数,求实数a的取值范围.
解:由已知得f'(x)=3x2-a,
因为f(x)在(-∞,+∞)上是增函数,
所以f'(x)=3x2-a≥0在(-∞,+∞)上恒成立,
即a≤3x2对x∈R恒成立,因为3x2≥0,所以只需a≤0.
又因为a=0时,f'(x)=3x2≥0,f(x)=x3-1在R上是增函数,所以a≤0.即a的取值范围为(-∞,0].
【母题探究】
1.(变条件)若函数f(x)=x3-ax-1在(-1,1)上单调递减,求a的取值范围.
解:由题意可知f'(x)=3x2-a≤0在(-1,1)上恒成立,所以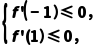 即
即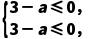
所以a≥3.
即a的取值范围是[3,+∞).
2.(变条件)若函数f(x)=x3-ax-1的单调递减区间为(-1,1),求a的值.
解:f'(x)=3x2-a,①当a≤0时,f'(x)≥0,
所以f(x)在(-∞,+∞)上为增函数,不满足题意.
②当a>0时,令3x2-a=0,得x=±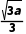
当-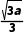 <x<
<x<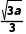 时,f'(x)<0.所以f(x)在(-
时,f'(x)<0.所以f(x)在(-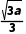 )上单调递减,
)上单调递减,
所以f(x)的单调递减区间为(-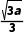 ),所以
),所以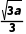 =1,即a=3.
=1,即a=3.
通性通法
由函数的单调性求参数的技巧
(1)转化为导数不等式恒成立问题:若f(x)在区间上单调递增(减),则f'(x)≥(≤)0恒成立,可以利用分离参数法或函数性质求参数,注意检验参数取“=”时是否满足题意;
(2)若f(x)在区间上不是单调函数,则解法通常有以下两种:
①转化为单调函数求参数,再求其补集;
②转化为函数的导函数有变号的零点,再求参数.
【跟踪训练】
1.(2024·青岛月考)若函数f(x)=ax-ln x在[1,2]上单调递增,则a的取值范围是()
A.(-∞,1]B.[1,+∞)
C.[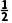 ,+∞)D.(-∞,]
,+∞)D.(-∞,]
解析:B f'(x)=a-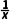 .因为f(x)在[1,2]上单调递增,所以f'(x)≥0对x∈[1,2]恒成立,即a≥
.因为f(x)在[1,2]上单调递增,所以f'(x)≥0对x∈[1,2]恒成立,即a≥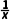 对x∈[1,2]恒成立,所以a≥(
对x∈[1,2]恒成立,所以a≥(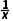 )max=1,即a∈[1,+∞).
)max=1,即a∈[1,+∞).
2.若函数f(x)=x3-12x在区间(k-1,k+1)上不单调,则实数k的取值范围是()
A.(-∞,-3]∪[-1,1]∪[3,+∞)
B.(-3,-1)∪(1,3)
C.(-2,2)
D.不存在这样的实数k
解析:B由题意得,f'(x)=3x2-12=0在区间(k-1,k+1)上至少有一个实数根.又f'(x)=3x2-12=0的根为±2,且f'(x)在x=2或-2两侧异号,而区间(k-1,k+1)的区间长度为2,故只有2或-2在区间(k-1,k+1)内,∴k-1<2<k+1或k-1<-2<k+1,∴1<k<3或-3<k<-1,故选B.
【例3】(1)(2024·郑州月考)已知函数f(x)=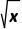 +ln x,则()
+ln x,则()
A.f(e)<f(π)<f(2.7)B.f(π)<f(e)<f(2.7)
C.f(e)<f(2.7)<f(π)D.f(2.7)<f(e)<f(π)
(2)已知函数f(x)=4x+3sin x,x∈(-1,1),若f(1-a)+f(1-a2)<0成立,则实数a的取值范围为()
A.(0,1)B.(1,)
C.(-2,-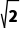 )D.(-∞,-2)∪(1,+∞)
)D.(-∞,-2)∪(1,+∞)
答案:(1)D(2)B
解析:(1)函数f(x)=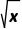 +lnx的定义域为(0,+∞).∵f'(x)=(
+lnx的定义域为(0,+∞).∵f'(x)=(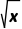 +lnx)'=(
+lnx)'=(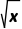 )'+(lnx)'=
)'+(lnx)'=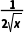 +
+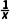 >0,∴f(x)在(0,+∞)上是增函数.∵2.7<e<π,∴f(2.7)<f(e)<f(π),故选D.
>0,∴f(x)在(0,+∞)上是增函数.∵2.7<e<π,∴f(2.7)<f(e)<f(π),故选D.
(2)∵f(x)=4x+3sinx,x∈(-1,1),∴f'(x)=4+3cosx>0在x∈(-1,1)上恒成立,∴f(x)在(-1,1)上单调递增.又f(x)=4x+3sinx,x∈(-1,1)是奇函数,∴不等式f(1-a)+f(1-a2)<0可化为f(1-a)<f(a2-1).结合函数f(x)的定义域可知,a要满足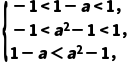 解得1<a<
解得1<a<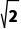 .
.
通性通法
比较大小及求函数不等式解集的一般思路
(1)在比较两数(式)的大小关系时,首先要判断所给函数的单调性,再根据函数的单调性比较大小,有时还需要根据待比较式的结构特征构造新的函数,由新函数的单调性来比较大小.
(2)对于利用导数解不等式问题,需要利用导数判断出函数的单调性,再利用单调性解不等式.注意函数定义域.
【跟踪训练】
1.已知实数x,y满足2x+2x<2y+2y,则()
A.x>yB.x=y
C.x<yD.x,y的大小不确定
解析:C设f(t)=2t+2t,所以f'(t)=2+2tln2>0,所以函数f(t)是增函数,由题意得f(x)<f(y),所以x<y.
2.如图所示的是函数f(x)=ax3+bx2+cx+d的图象,f'(x)为函数f(x)的导函数,则不等式x·f'(x)<0的解集为{x|x<-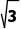 或0<x<
或0<x<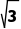 }.
}.
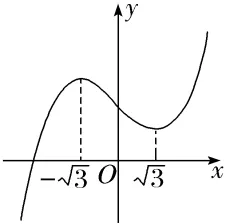
解析:由f(x)的图象知,f(x)在(-∞,-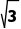 )和(
)和(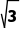 ,+∞)上单调递增,在(-
,+∞)上单调递增,在(-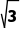 )上单调递减,所以当x∈(-∞,-
)上单调递减,所以当x∈(-∞,-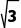 )∪(
)∪(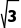 ,+∞)时,f'(x)>0;当x∈(-
,+∞)时,f'(x)>0;当x∈(-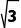 )时,f'(x)<0.所以x·f'(x)<0的解集为{x|x<-
)时,f'(x)<0.所以x·f'(x)<0的解集为{x|x<-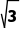 或0<x<
或0<x<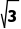 }.
}.

1.设函数f(x)=2x+sin x,则()
A.f(1)>f(2)B.f(1)<f(2)
C.f(1)=f(2)D.以上都不正确
解析:B f'(x)=2+cosx>0,故f(x)是R上的增函数,故f(1)<f(2).
2.若函数f(x)=-cos x+ax为增函数,则实数a的取值范围为()
A.[-1,+∞)B.[1,+∞)
C.(-1,+∞)D.(1,+∞)
解析:B由题意可得,f'(x)=sinx+a≥0恒成立,故a≥-sinx恒成立,因为-1≤-sinx≤1,所以a≥1.
3.(2024·温州月考)已知函数f(x)=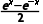 f(a+3)>f(2a),则a的取值范围是(-∞,3).
f(a+3)>f(2a),则a的取值范围是(-∞,3).
解析:由函数f(x)=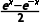 f'(x)=
f'(x)=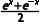 >0,即f(x)为R上的增函数,故由f(a+3)>f(2a)可得a+3>2a,∴a<3.
>0,即f(x)为R上的增函数,故由f(a+3)>f(2a)可得a+3>2a,∴a<3.
4.已知函数f(x)=x3+ax2-a2x+2(a>0).求函数f(x)的单调区间.
解:f'(x)=3x2+2ax-a2=(x+a)(3x-a),由f'(x)=0得x=-a或x=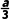 .
.
又a>0,由f'(x)<0,得-a<x<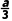 f'(x)>0,得x<-a或x>
f'(x)>0,得x<-a或x>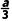
故f(x)的单调递减区间为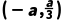
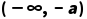 和
和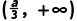 .
.


1.已知函数f(x)=3x-ax(a∈R),则“a<0”是“函数f(x)为增函数”的()
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
解析:A因为f(x)=3x-ax,所以f'(x)=3xln3-a,所以当a≤0时,f'(x)>0,函数f(x)在定义域上是增函数.因为(-∞,0)⫋(-∞,0],所以“a<0”是“函数f(x)为增函数”的充分不必要条件.故选A.
2.若f(x)=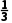 x3-ax2的单调递减区间是(0,2),则正数a的值是()
x3-ax2的单调递减区间是(0,2),则正数a的值是()
A.1B.2
C.3D.4
解析:A f'(x)=x2-2ax,令f'(x)<0,由于a>0,故解得0<x<2a,故2a=2,即a=1.
3.若函数f(x)=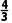 x3-2ax2-(a-2)x+5恰好有三个单调区间,则实数a的取值范围为()
x3-2ax2-(a-2)x+5恰好有三个单调区间,则实数a的取值范围为()
A.-1≤a≤2B.-2≤a≤1
C.a>2或a<-1D.a>1或a<-2
解析:D若函数f(x)有3个单调区间,则f'(x)=4x2-4ax-(a-2)有2个零点,故Δ=16a2+16(a-2)>0,解得a>1或a<-2.
4.(2024·温州期中)已知函数f(x)=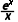 <x<3时,下列关系正确的是()
<x<3时,下列关系正确的是()
A.f(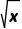 )<f(x)<[f(x)]2
)<f(x)<[f(x)]2
B.f(x)<f(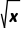 )<[f(x)]2
)<[f(x)]2
C.[f(x)]2<f(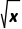 )<f(x)
)<f(x)
D.[f(x)]2<f(x)<f(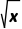 )
)
解析:A由题意得f'(x)=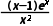 1<x<3时,f'(x)>0,所以f(x)在(1,3)上单调递增.又1<
1<x<3时,f'(x)>0,所以f(x)在(1,3)上单调递增.又1<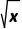 <x<3,所以f(
<x<3,所以f(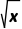 )<f(x).由f(x)在(1,3)上单调递增,可知当x∈(1,3)时,f(x)>f(1)=e,所以[f(x)]2>f(x).综上f(
)<f(x).由f(x)在(1,3)上单调递增,可知当x∈(1,3)时,f(x)>f(1)=e,所以[f(x)]2>f(x).综上f(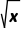 )<f(x)<[f(x)]2.
)<f(x)<[f(x)]2.
5.(多选)已知定义在R上的函数f(x),其导函数y=f'(x)的大致图象如图所示,则下列叙述正确的是()
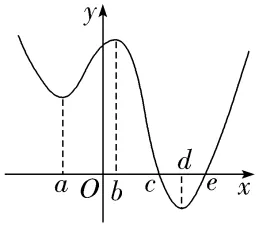
A.f(b)>f(a)B.f(d)>f(e)
C.f(a)>f(d)D.f(c)>f(e)
解析:ABD由题图可得,当x∈(-∞,c)∪(e,+∞)时,f'(x)>0,当x∈(c,e)时,f'(x)<0,故f(x)在(-∞,c),(e,+∞)上单调递增,在(c,e)上单调递减,所以f(b)>f(a),f(d)>f(e),f(c)>f(e).
6.(多选)若函数f(x)=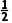 x2-9ln x,在区间[m-1,m+1]上单调,则实数m的取值可以是()
x2-9ln x,在区间[m-1,m+1]上单调,则实数m的取值可以是()
A.4B.3
C.2D.1
解析:AC f(x)的定义域为(0,+∞),f'(x)=x-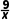 =
=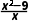 ;由f'(x)≥0得函数f(x)的单调递增区间为[3,+∞);由f'(x)≤0得函数f(x)的单调递减区间为(0,3];因为f(x)在区间[m-1,m+1]上单调,所以
;由f'(x)≥0得函数f(x)的单调递增区间为[3,+∞);由f'(x)≤0得函数f(x)的单调递减区间为(0,3];因为f(x)在区间[m-1,m+1]上单调,所以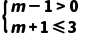 或m-1≥3,解得1<m≤2或m≥4;结合选项可得A、C正确.
或m-1≥3,解得1<m≤2或m≥4;结合选项可得A、C正确.
7.函数f(x)=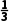 x3-
x3-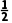 (2a+1)x2+(a2+a)x+4(a∈R)的单调递减区间是(a,a+1).
(2a+1)x2+(a2+a)x+4(a∈R)的单调递减区间是(a,a+1).
解析:f'(x)=x2-(2a+1)x+a2+a=[x-(a+1)](x-a),令f'(x)<0,得a<x<a+1,故f(x)的单调递减区间是(a,a+1).
8.若f(x)=x3-ax2+4在(0,2)内单调递减,则实数a的取值范围是[3,+∞).
解析:f'(x)=3x2-2ax,∵f(x)在(0,2)内单调递减,∴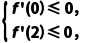 ∴
∴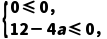 ∴a≥3.
∴a≥3.
9.(2024·厦门月考)若函数f(x)=2x-sin x,则满足f(2x-1)>f(x+1)的实数x的取值范围是(2,+∞).
解析:∵f'(x)=2-cosx>0,∴f(x)=2x-sinx在R上是增函数,又∵f(2x-1)>f(x+1),∴2x-1>x+1,解得x>2.
10.已知函数f(x)=aln x+x,讨论f(x)的单调性.
解:∵f(x)=alnx+x(x>0),
∴f'(x)=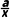 +1=
+1=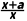 (x>0),
(x>0),
若a≥0,则f'(x)>0,函数f(x)在(0,+∞)上为增函数;
若a<0,则当x∈(-a,+∞)时,f'(x)>0,当x∈(0,-a)时,f'(x)<0,
∴f(x)在(-a,+∞)上单调递增,在(0,-a)上单调递减.
综上,当a≥0时,f(x)在(0,+∞)上为增函数;
当a<0时,f(x)在区间(-a,+∞)上单调递增,在区间(0,-a)上单调递减.

11.已知函数f(x)=ax-ex在(0,1)上不是单调函数,则实数a的取值范围是()
A.(0,1)B.(0,e)
C.(1,e)D.(-∞,e)
解析:C f'(x)=a-ex.因为f(x)=ax-ex在(0,1)上不单调,所以f'(x)=0在(0,1)上有解,又f'(x)在(0,1)上单调递减,所以f'(0)=a-1>0,f'(1)=a-e<0,故a∈(1,e).故选C.
12.(2024·广州月考)已知函数f(x)=2sin x-ex+e-x,则关于x的不等式f(x2-4)+f(3x)<0的解集为()
A.(-4,1)B.(-1,4)
C.(-∞,-4)∪(1,+∞)D.[-1,4]
解析:C f(-x)=-2sinx-e-x+ex,∵f(-x)+f(x)=0,∴f(x)为奇函数,则f'(x)=2cosx-(ex+e-x),∵2cosx≤2,ex+e-x≥2,∴f'(x)≤0,f(x)为减函数,又f(x2-4)+f(3x)<0,则f(x2-4)<-f(3x)=f(-3x),∴x2-4>-3x,∴x>1或x<-4.故选C.
13.已知奇函数f(x)的定义域为R,且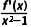 >0,则f(x)的单调递减区间为(-1,1);满足以上条件的一个函数是f(x)=
>0,则f(x)的单调递减区间为(-1,1);满足以上条件的一个函数是f(x)=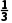 x3-x(答案不唯一).
x3-x(答案不唯一).
解析:由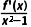 >0,可得f'(x)(x2-1)>0,所以
>0,可得f'(x)(x2-1)>0,所以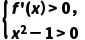 或
或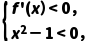 所以当x<-1或x>1时,f'(x)>0,当-1<x<1时,f'(x)<0,所以f(x)的单调递减区间为(-1,1).满足条件的一个函数可以为f(x)=
所以当x<-1或x>1时,f'(x)>0,当-1<x<1时,f'(x)<0,所以f(x)的单调递减区间为(-1,1).满足条件的一个函数可以为f(x)=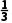 x3-x.
x3-x.
14.已知函数f(x)=ax2+ln(x+1).
(1)当a=-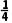 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)若函数f(x)在区间[1,+∞)上单调递减,求实数a的取值范围.
解:(1)当a=-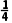 时,f(x)=-
时,f(x)=-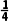 x2+ln(x+1)(x>-1),
x2+ln(x+1)(x>-1),
则f'(x)=-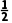 x+
x+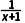 =-
=-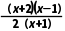 (x>-1).
(x>-1).
令f'(x)>0,解得-1<x<1;
令f'(x)<0,解得x>1.
故函数f(x)的单调递增区间是(-1,1),单调递减区间是(1,+∞).
(2)因为函数f(x)在区间[1,+∞)上单调递减,所以f'(x)=2ax+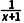 ≤0对任意x∈[1,+∞)恒成立,即a≤-
≤0对任意x∈[1,+∞)恒成立,即a≤-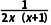 对任意x∈[1,+∞)恒成立.
对任意x∈[1,+∞)恒成立.
令g(x)=-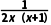 ∈[1,+∞),
∈[1,+∞),
易求得g'(x)>0在[1,+∞)上恒成立,
所以g(x)在[1,+∞)上单调递增,
因此g(x)min=g(1)=-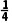 a≤-
a≤-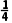 .
.
即实数a的取值范围是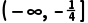 .
.

15.已知函数f(x)=e|x|+cos x,则不等式f(2x)≤f(x-1)的解集为{x|-1≤x≤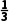 }.
}.
解析:函数f(x)的定义域为R,f(-x)=e|-x|+cos(-x)=e|x|+cosx=f(x),所以函数f(x)为偶函数.当x≥0时,f(x)=ex+cosx,f'(x)=ex-sinx≥1-sinx≥0,所以函数f(x)在区间[0,+∞)上单调递增,由f(2x)≤f(x-1)可得f(|2x|)≤f(|x-1|),所以|2x|≤|x-1|,则有4x2≤(x-1)2,得3x2+2x-1≤0,解得-1≤x≤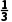 .所以不等式的解集为{x|-1≤x≤
.所以不等式的解集为{x|-1≤x≤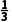 }.
}.
16.(2024·宁波月考)设函数f(x)=(x+a)ln x,g(x)=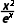 .已知曲线y=f(x)在点(1,f(1))处的切线与直线2x-y=0平行.
.已知曲线y=f(x)在点(1,f(1))处的切线与直线2x-y=0平行.
(1)求a的值;
(2)是否存在自然数k,使得方程f(x)=g(x)在(k,k+1)内存在唯一的根?如果存在,求出k;如果不存在,请说明理由.
解:(1)由题意知,曲线y=f(x)在点(1,f(1))处的切线斜率为2,所以f'(1)=2,
又f'(x)=lnx+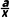 +1,
+1,
所以a+1=2,解得a=1.
(2)存在.
设h(x)=f(x)-g(x)=(x+1)lnx-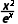
当x∈(0,1]时,h(x)<0,
又h(2)=3ln2-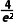 =ln8-
=ln8-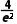 >0,
>0,
所以存在x0∈(1,2),使得h(x0)=0.
因为h'(x)=lnx+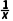 +1+
+1+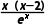
当x∈(1,2)时,h'(x)>1-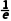 >0,
>0,
当x∈[2,+∞)时,h'(x)>0,
所以当x∈(1,+∞)时,h(x)单调递增.
所以当k=1时,方程f(x)=g(x)在(k,k+1)内存在唯一的根.

通过网盘分享的文件:25-26学年同步培优讲义
链接: https://pan.baidu.com/s/1y0bSGZE1YoJg8gMTXiqQoA?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享