 年普通高等学校招生全国统一考试(天津卷回忆版)
年普通高等学校招生全国统一考试(天津卷回忆版)
数学
本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.第1卷1至3页第Ⅱ卷4至6页.
答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上,并在规定位置粘贴考试用条形码.答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效.考试结束后,将本试卷和答题卡一并交回.在天津考生获取更多学习资料祝各位考生考试顺利!
第I卷(选择题)
注意事项:
1.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.
2.本卷共9小题,每小题5分,共45分.
参考公式:
·如果事件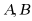 互斥,那么
互斥,那么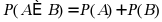
·如果事件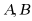 相互独立,那么
相互独立,那么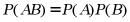
·棱柱的体积公式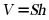 ,其中S表示棱柱的底面面积,h表示棱柱的高.
,其中S表示棱柱的底面面积,h表示棱柱的高.
·圆锥的体积公式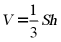 ,其中S表示圆锥的底面面积,h表示圆锥的高.
,其中S表示圆锥的底面面积,h表示圆锥的高.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的
1. 已知集合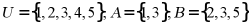 ,则
,则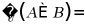 ()
()
A. B. C. D.
【答案】D
【解析】
【分析】由集合的并集、补集的运算即可求解.
【详解】由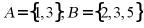 ,则
,则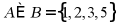
集合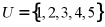
故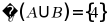
故选:D.
2. 设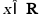 ,则“
,则“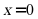 ”是“
”是“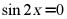 ”的()
”的()
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
【答案】A
【解析】
【分析】通过判断是否能相互推出,由充分条件与必要条件的定义可得.
【详解】由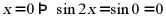 ,则“
,则“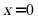 ”是“
”是“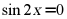 ”的充分条件;
”的充分条件;
又当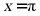 时,
时,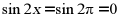 ,可知
,可知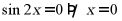
故“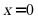 ”不是“
”不是“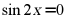 ”的必要条件,
”的必要条件,
综上可知,“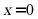 ”是“
”是“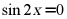 ”的充分不必要条件.
”的充分不必要条件.
故选:A.
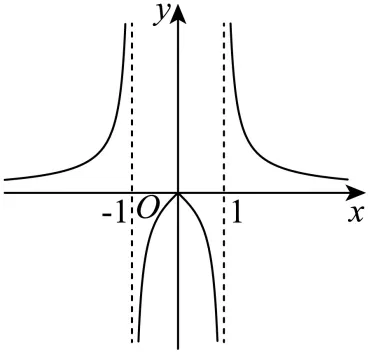
3. 已知函数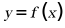 的图象如下,则
的图象如下,则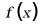 的解析式可能为()
的解析式可能为()
A. 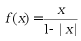 B.
B. 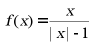 C.
C. 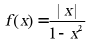 D.
D. 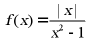
【答案】D
【解析】
【分析】先由函数奇偶性排除AB,再由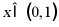 时函数值正负情况可得解.
时函数值正负情况可得解.
【详解】由图可知函数为偶函数,而函数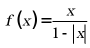 和函数
和函数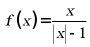 为奇函数,故排除选项AB;
为奇函数,故排除选项AB;
又当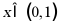 时
时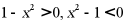 ,此时
,此时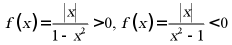
由图可知当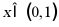 时,
时,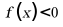 ,故C不符合,D符合.
,故C不符合,D符合.
故选:D
4. 若m为直线,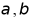 为两个平面,则下列结论中正确的是()
为两个平面,则下列结论中正确的是()
A. 若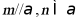 ,则
,则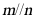 B. 若
B. 若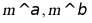 ,则
,则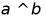
C. 若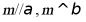 ,则
,则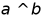 D. 若
D. 若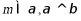 ,则
,则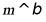
【答案】C
【解析】
【分析】根据线面平行的定义可判断A的正误,根据空间中垂直关系的转化可判断BCD的正误.
【详解】对于A,若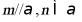 ,则
,则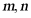 可平行或异面,故A错误;
可平行或异面,故A错误;
对于B,若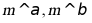 ,则
,则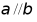 ,故B错误;
,故B错误;
对于C,若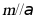 ,则存在直线
,则存在直线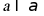
所以由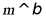 可得
可得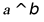 ,故
,故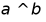 ,故C正确;
,故C正确;
对于D,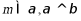 ,则
,则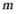 与
与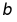 可平行或相交或
可平行或相交或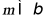 ,故D错误;
,故D错误;
故选:C.
5. 下列说法中错误的是()
A. 若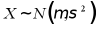 ,则
,则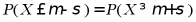
B. 若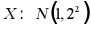 ,则
,则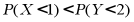
C
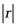 越接近1,相关性越强
越接近1,相关性越强
D. 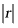 越接近0,相关性越弱
越接近0,相关性越弱
【答案】B
【解析】
【分析】根据正态分布以及相关系数的概念直接判断即可.
【详解】对于A,根据正态分布对称性可知,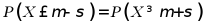 说法正确;
说法正确;
对于B,根据正态分布对称性可知,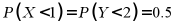 说法错误;
说法错误;
对于C和D,相关系数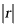 越接近0,相关性越弱,越接近1,相关性越强,故C和D说法正确.
越接近0,相关性越弱,越接近1,相关性越强,故C和D说法正确.
故选:B
6. 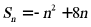 ,则数列
,则数列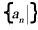 的前
的前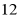 项和为()
项和为()
A 112B. 48C. 80D. 64
112B. 48C. 80D. 64
【答案】C
【解析】
【分析】先由题设结合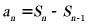 求出数列
求出数列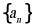 的通项公式,再结合数列
的通项公式,再结合数列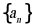 各项正负情况即可求解.
各项正负情况即可求解.
【详解】因为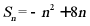
所以当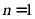 时,
时,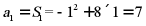
当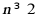 时,
时,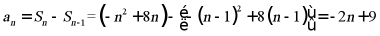
经检验,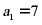 满足上式,
满足上式,
所以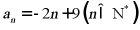 ,令
,令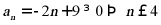
设数列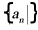 的前n项和为
的前n项和为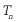
则数列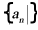 的前
的前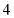 项和为
项和为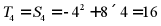
数列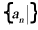 的前
的前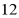 项和为
项和为
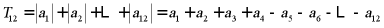
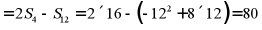 .
.
故选:C
7. 函数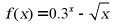 的零点所在区间是()
的零点所在区间是()
A
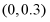 B.
B. 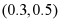 C.
C. 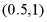 D.
D. 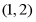
【答案】B
【解析】
【分析】利用指数函数与幂函数的单调性结合零点存在性定理计算即可.
【详解】由指数函数、幂函数的单调性可知: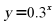 在
在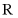 上单调递减,
上单调递减,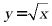 在
在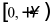 单调递增,
单调递增,
所以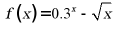 在定义域上单调递减,
在定义域上单调递减,
显然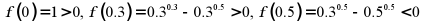 ,
,
所以根据零点存在性定理可知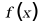 的零点位于
的零点位于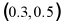 .
.
故选:B
8. 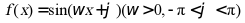 ,在
,在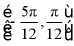 上单调递增,且
上单调递增,且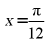 为它的一条对称轴,
为它的一条对称轴,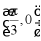 是它的一个对称中心,当
是它的一个对称中心,当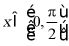 时,
时,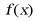 的最小值为()
的最小值为()
A. 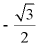 B.
B. 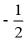 C. 1D. 0
C. 1D. 0
【答案】A
【解析】
【分析】利用正弦函数的对称性得出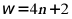 ,根据单调性得出
,根据单调性得出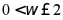 ,从而确定
,从而确定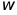 ,结合对称轴与对称中心再求出
,结合对称轴与对称中心再求出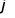 ,得出函数解析式,利用整体思想及正弦函数的性质即可得解.
,得出函数解析式,利用整体思想及正弦函数的性质即可得解.
【详解】因为函数在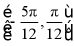 上单调递增,且
上单调递增,且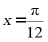 为它的一条对称轴,
为它的一条对称轴,



通过网盘分享的文件:【免费下载】高考真题【天津】2025年高考天津卷数学真题(解析版)word版含解析学生版教师版
链接: https://pan.baidu.com/s/1TdKQBrcf9CR_dSQrp_yuew?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享